들어가며
한참 generative 모형으로서 GAN이 화제가 되었던 17년 초에 사내에서 세미나를 진행하면서 처음 접하게 되었습니다. 뜨거웠던 GAN보다도 제가 개인적으로 variational autoencoder(이하 VAE)에 대해 관심을 가지게 된 것은 deep learning 분야 중에서 가장 통계적인 background가 많이 필요하다는 사실 때문이었습니다. 제가 부서 내 통계를 담당하고 있거든요. ㅎㅎ~~ 처음에는 막연히 autoencoder의 일종이겠구나 하면서 논문을 읽기 시작했는데, 실은 autoencoder와는 전혀 다른 것이었고, 아주 흥미로운 모형이었습니다. 최초 사내 세미나 진행 후 몇 번을 다시 읽으며 개념을 정리했습니다. 혹시 관심 있으셨지만, 많은 시간을 들여 논문을 읽기 힘드신 분들에게는 개념 잡는 데 도움이 되기를 바랍니다.
글을 적다가 보니 너무 길어지는 면이 있어서, warming-up 차원에서 첫 두 부분은 VAE와 관련된 잡기적인 내용들을 다루어 보겠습니다. 제가 알지 못하는 그 무언가가 있을 수도 있고, 동의하기 어려울 수 있는 개인적인 의견이 많이 포함되어 있다는 말씀을 먼저 드립니다. 혹시 그런 면이 있다면 알려주세요. 바로 수정에 들어갑니다..^^
VAE는 Auto-Encoding Variational Bayes라는 이름으로 최초 13년 12월에 The Journal of Machine Learning Research에 submit된 논문이구요. 18년 5월 현재 2071번이나 cite된 대단한 논문입니다. 4년도 넘게 지난 시점에서 그 모형을 공부하게 되다니. 다시 한번 저의 게으름을 반성하게 됩니다. 하지만, 제가 알기로는 본격적으로 회자되었던 시점은 17년 초반이구요. 이는 GAN이 인구에 회자되는 시점이었습니다. 참고로 GAN도 14년 10월에 나온 논문이네요. 앞으로 이 논문도 심도있게 알기 쉽게 정리해 보도록 하죠.
먼저 개인적으로 VAE라고 하면 제일 먼저 떠오르는 단어는 generative model이라는 단어입니다. VAE를 한마디로 줄이자면, 데이터를 학습해서 데이터와 비슷하지만, 존재하지 않는 데이터를 생성해 내기 위한 모형입니다. 데이터를 생성해 내기 위해서는 무엇을 알아야 할까요? 데이터를 만들어내는 mechanism을 알아야 하는데, 우리가 숫자 그림을 다시 생성해 내자고 숫자를 적을 수 있는 팔과 머리를 만들어낼 수는 없는 노릇입니다. 실제 데이터 관점에서 우리가 할 수 있는 일은 데이터가 어떤 형태로 퍼져 있는지를 잘 파악하는 것입니다. 그리고 그 분포에 따라 그림을 잘 복원해 내는 것입니다. machine learning에서는 실제로 데이터의 분포를 안다는 것과 데이터의 생성 메커니즘을 안다는 것을 같은 의미로 사용합니다.
확률분포를 보는 두개의 시선
machine learning(이하 ML)에서는 분포를 단순히 하나의 mapping이라고 생각합니다. 이는 전통적인 통계에서 확률분포를 대하는 것과는 조금 다른 관점을 지닙니다. 통계학에서는 분포를 통해 확률을 계산하고, 불확실성을 통제 혹은 표현하기 위한 용도로 사용합니다. 예를 들면, 어떠한 가정 하에서 실제 데이터가 발생할 확률을 바탕으로 p-value를 구합니다. 이 p-value를 바탕으로 가설을 검정합니다.
p-value가 ML에서는 더이상 제 역할을 하기 힘들고, 이에 대한 맹신을 경계하는 statement가 ASA(American Statistical Assosiation)로부터 나오기도 했습니다. (관련해서는 따로 포스팅 해보려 합니다.)

불확실성을 control하는 좋은 예는 표본 조사를 진행할 때, 샘플의 개수를 구하는 문제입니다. 확률 분포를 가정하고, 그 확률분포가 사실일 때, 과연 몇 개의 표본을 관찰하면, 오차(error)를 원하는 수준으로 유지할 수 있을까를 계산합니다. 통계량의 확실성을 표현해 주는 예로는 신뢰구간이 있습니다. 여러분이 모두 알고 계실만한 회귀분석에서는 회귀계수를 추정한 후에 그 회귀 계수가 통계적으로 얼마나 믿을만 한지를 회귀계수의 신뢰구간으로 표현합니다. 워낙 일반적인 내용이라 다룰 필요 없겠지만, 시간이 되면 정리하는 차원에서 한번 다루도록 하겠습니다. 어쨌든, 통계에서는 확률분포를 불확실성을 표현하는 수단입니다.
ML에서는 확률로서의 분포는 크게 중요하게 여기지 않습니다.그래서 ML 모형들은 분석할 때 확률분포를 가정하지 않는 경우가 많습니다. 그리고 당연히 예측의 quality에 대해서는 분포로 말하지 않습니다. 실제 데이터와 예측을 비교한 contingency table을 이용해서 error rate(type I error와 type II error 혹은 sensitivity analysis)과 그 변형 지표만으로 불확실성을 표현합니다. 반면 통계에서는 가정으로부터 도출된 통계량(statistic)의 확률분포로 유의미한지 무의미한지를 측정합니다.
ML에서는 매 관측치마다 얻는 확률도 empirical 확률일 경우가 많습니다. 분류 문제를 풀 때, Random forest 모형의 최종 결과물로 나오는 확률은 그냥 여러 개의 작은 모형으로부터 얻은 결과의 평균에 지나지 않습니다. SVM도 사실은 hyperplane을 중심으로 어디에 속하는지만 중요하며, 관측치의 membership만 예측합니다. scikit-learn package에 분류 확률을 구해주는 옵션이 있기는 하지만, 사후적으로 hyperplane에서 얼마나 먼지를 표현하는 정도일 뿐입니다. ML에서의 확률 개념은 이렇듯 중요한 요소가 아니며, 확률분포도 실제 데이터가 퍼져 있는 모양을 표현하는 수단으로 여깁니다. VAE에서도 마찬가지 입니다.
제 생각에 ML은 통계학에 비해서 좀더 유연한 면이 많습니다. 통계학에서는 불확실성을 통제하려고 하지만, ML에서는 불확실성을 통제하려 하기보다는 기술하려고 하는 입장에 더 가까운 것 같습니다. 그렇다 보니, 확률 분포를 그 자체가 의미를 가지는 분포로 이해하기 보다는 mapping으로 이해하게 되는 것이죠. 이런 사상이 극대화 되어 나타나는 것이 manifold hypothesis일 것입니다.
Manifold hypothesis
보통 우리가 보는 데이터는 사실 수학적으로 보면 아주 작은 공간에 몰려 있다고 볼 수 있습니다. $28 \times 28$ 차원짜리 MNIST 손글씨 이미지만 하더라도, 784차원의 데이터이고, 이 784차원의 데이터가 표현할 수 있는 흑백 이미지는 $255^{784}$개에 이릅니다만, 실제 숫자라는 의미를 지닌 이미지의 가짓수는 그렇게 많지는 않을 것입니다. 그러므로, 아무리 복잡해 보이는 데이터라도 그 구조만 확실하게 존재한다고 하면, 아주 작은 차원의 데이터로 표현할 수 있다고 하는 것인 deep learning에서 이야기하는 manifold hypothesis입니다.
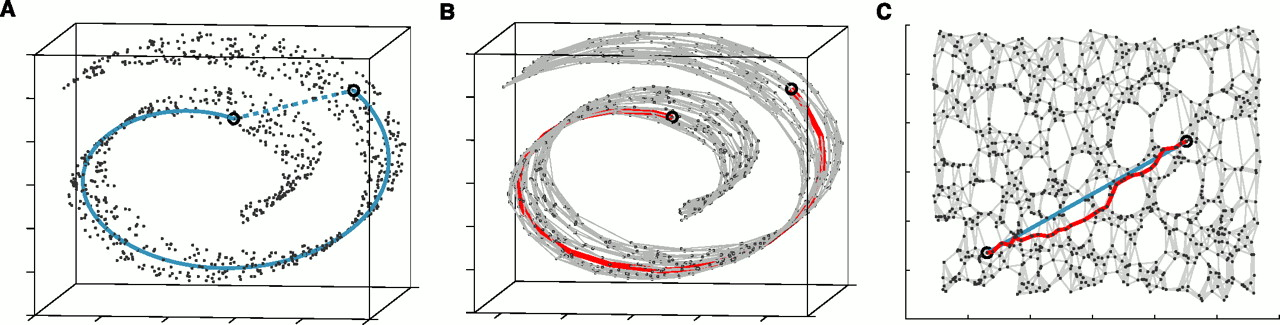
A Global Geometric Framework for Nonlinear Dimensionality Reduction Joshua B. Tenenbaum, Vin de Silva, John C. Langford
위의 그림은 manifold의 개념을 가장 잘 설명해주는 그림 중의 하나입니다. 우리가 익숙한 3차원 공간에 데이터가 swiss roll 형태로 모여 있다고 하죠. 단순히 두 점의 거리를 Euclidean distance로 재면 그림 A의 점선으로 표시할 수 있습니다. 하지만, 데이터를 가장 잘 설명하는 2차원 manifold를 찾으면, 그림 B에서 보이는 것처럼 데이터를 그 manifold 위에서 설명할 수 있습니다. 이 manifold를 펴면, 그리고 그 위에서 정의된 euclidean distance는 그림 C의 청록색 선으로 표시할 수 있습니다. 데이터 공간에서의 거리보다 manifold 위에서의 거리가 훨씬 크다는 것을 알 수 있습니다. 언뜻 비슷해 보이는 그림이라도 실제 공간에서는 아주 다른 그림일 수 있는 것입니다. 만약 동물의 이미지를 제대로 표현할 수 있는 manifold라면, 강아지 이미지들과의 거리가 사진에 찍히기를 언뜻 강아지 같아 보이는 고양이의 그림과의 거리는 훨씬 짧다는 것이죠.
위의 경우에서처럼, 경우에 따라서는 원래 데이터의 공간은 큰 의미가 없을 수도 있습니다. 이런 경우 manifold는 원래 데이터 공간과는 판이하게 다를 수 있있겠죠. 그래서 ML에서는 원래 공간에서 확률분포를 추정하려는 시도조차 하지 않는 것 같습니다. SVM은 오히려 공간을 확장함으로써 보다 쉬운 hyperplane을 찾아내려고 노력하고, VAE에서는 대신 우리가 handling할 수 있는 훨씬 작은 차원에 속하는 manifold를 찾아내고 그 manifold에 데이터를 잘 mapping하는 것이 아주 중요한 관심사가 된 것이죠.
마치며
지금까지의 이야기를 정리하면, 데이터의 분포를 사람이 이해할 수 있거나, 최소한 다룰 수 있는 작은 공간에서 잘 파악해보자는 것이 VAE의 목적입니다. 이 과정에서 variational inference라는 기법을 활용하는 것이구요.
다음 글에서는 좀더 본격적으로 VAE에 대해서 살펴보도록 하겠습니다.