Variational Autoencoder (III)

최우추정 원리

우리가 추정해야 할 모수는 $\zeta$, $\theta$입니다. 각각 encoder 신경망과 decoder 신경망의 weight 값을 의미합니다. 잠재변수의 사후분포(posterior distribution)의 모수인 $\mu$와 $\sigma$는 $\zeta$가 정해지면 같이 정해지는 숫자이며, 실제 잠재변수를 표현할 때에는 이 모수들을 이용해서 시각화 할 것입니다. $f(z;\theta)$가 결정이 되면 여기에 약간 noise를 더한 값이 생성하는 이미지가 됩니다. VAE에서 궁극적으로 하고자 하는 것은 최대 우도 원칙(Maximum Likliohood Principle)에 의거해서 데이터의 분포를 추정하는 것입니다. 다음은 우도함수(우도함수)의 정의입니다. $P(X;\nu) = L(\nu; X)$ $X$는 데이터를 의미합니다. $\nu$는 추정하고자 하는 모수(parameter)를 의미합니다. 우도함수와 확률분포 함수는 동일한 함수로, 보는 관점만 다르다고 볼 수 있습니다. 확률분포는 사상(Event)가 발생할 확률을 assign하는 원칙을 정의하는 것으로, 데이터가 나올 확률을 가장 크게 해주는 모수를 찾고자 한다면, 우도함수로 이해할 수 있습니다.

만약, 다수의 관측치가 있고, 관측치 사이에 독립성 가정이 주어졌을 경우, 다음과 같이 쓸 수 있습니다.

$$L(\theta; X) = \prod_{i=1}^n p(x_i;\theta)$$

이 최대우도 원리는 생성 모형이 출현하면서 deep learning의 알고리즘을 이해하기 위해 필수적인 요소가 되어가고 있습니다. 인공지능의 빙하기를 깬 Restricted Boltzmann Machine에서 많이 사용된 이후, 한동안 분류 문제가 많이 대두됐던 지난 몇년 동안에는 확률분포와 MLE 원리가 그렇게 중요한 개념이 아니었습니다. 예측 성능을 높이기 위해 MSE와 categorical entropy를 줄이면 되는 상황이었습니다. 하지만, VAE와 GAN을 중심으로한 생성 모형이 중요한 연구 대상이 되면서, 데이터를 생성해 내는 분포를 추정해야 됨에 따라, 이제는 생성 모형의 알고리즘을 이해하기 위해서는 확률분포에 대한 이해가 아주 중요한 부분이 되었습니다.

이제 우리가 찾아야 하는 모수, $\zeta, \theta$의 최우추정량들을 찾아보도록 하겠습니다.

최우 추정치를 찾기 위해 VAE에서는 Variational Inference라는 방법을 사용합니다. 이름에도 나와 있습니다. 그러므로, VAE에 대해 깊이 이해하기 위해서는 Variational Inference(VI)를 제대로 이해해야 합니다. VI는 EM 알고리즘과 비슷하게 닮아 있지만, 일치하지는 않습니다. EM 알고리즘은 hidden variable과 hidden variable이 주어진 경우의 conditional distribution을 명확히 가정하여, 최종적으로는 관측된 data의 확률 성질을 알고 싶은 것이 가장 큰 목적입니다만, VI는 통계적인 분포를 추정하기 위한 방법론이라기 보다는 함수 근사(function approximation)의 도구로 주로 사용됩니다. variational inference에 대해서 알아보도록 하겠습니다.

Variational Inference 알고리즘

최대화하기 어려운 marginal 우도함수 대신에 최대하기 쉬운 우도함수의 lower bound를 찾아내서, 이를 극대화하고자 하는 것이 EM 알고리즘의 key idea입니다. 이를 위해 EM 알고리즘에서는 data 생성 과정을 모델링하지만, VI는 하한을 극대화한다는 아이디어만 차용합니다. 다음과 같이 marginal 우도함수를 분해할 수 있습니다.

$$p(x) = \sum_z p(x, z) = \sum_z q (z\vert x) \frac{p (x,z)}{q(z\vert x)} = E_{Q(Z\vert x)}\left[\frac {p (x, Z)}{q(Z\vert x)}\right]$$

두 개의 서로 다른 parameter set, ($\phi, \theta$)를 가지고 있는 경우에 이를 적용하면 다음과 같은 결과를 얻을 수 있습니다.

$$\log p(x) = \log E_{Q_\phi (Z\vert x)}\left[\frac {p (x, Z)}{q(Z\vert x)}\right]\ge E_{Q (Z\vert x)}\left[\log\frac {p (x, Z)}{q(Z\vert x)}\right]$$

오른쪽의 식이 KL divergence, $- D_{KL}{Q(Z\vert X= x) | P(x, Z)}$와 일치하는군요.

KL divergence의 정의로부터, 먼저 marginal 우도함수를 뽑아내면, 맨 아래처럼 두개의 요소로 분리할 수 있습니다.

$$\begin{array}{ll} D_{KL}( Q_\phi(Z\vert x) \vert \vert P_\theta(Z\vert x)) &= \sum_z \log \frac{q_\phi(z\vert x)}{p_\theta(z\vert x)} q_\phi(z\vert x)\\ &= \int \log \frac{q_\phi(z\vert x)p(x)}{p_\theta(z,x)} q_\phi(z\vert x)dz\\ &= \int \log \frac{q_\phi(z\vert x)}{p_\theta(z,x)} q_\phi(z\vert x)dz + \log p_\theta(x)\underbrace{\sum_z q_\phi(z,x)}_{1}\\ &= \log p_\theta(x) + \underbrace{E_{q_\phi (z\vert x)}[\log q_\phi(z\vert x)] - E_{q_\phi (z\vert x)}[\log p_\theta(z,x)]}_{\mathcal L(\theta, \phi; x)} \end{array}$$

$\mathcal L(\theta, \phi; x)$을 왼쪽으로 넘기면,

$$\begin{array}{ll} \log p_\theta(x) &= - E_{Q_\phi (Z\vert x)}[\log q_\phi(Z\vert x)] + E_{Q_\phi (Z\vert x)}[\log p_\theta(Z,x)] + D_{KL}( Q_\phi(Z\vert x) \vert \vert P_\theta (Z\vert x))\\ & \ge \underbrace{- E_{Q_\phi (Z\vert x)}[\log q_\phi(Z\vert x)] + E_{Q_\phi (Z\vert x)}[\log p_\theta(Z,x)]}_{ELBO} \end{array}$$

이라는 결과를 얻는데, 우리는 마지막 줄의 결과물을 ELBO(Evidence Lower BOund)라고 부릅니다. KL divergence는 항상 0보다 크거나 같은 값을 가지므로, ELBO는 언제나 주변(marginal) 우도함수보다 작습니다. ELBO는 우도함수와 KL divergence와의 gap을 의미하기도 합니다. ELBO는 잠재 확률변수의 기대값으로 표현을 할 수 있고, 잠재 변수는 상대적으로 작은 차원을 가지고 있으므로, 주변 우도함수 대신 ELBO를 극대화하는 전략을 취하는 것이 계산상 유리합니다.

Variational Inference와 AutoEncoder

이제부터 이 VI가 어떻게 Autoencoder와 연결이 되는지에 대해서 알아보도록 하겠습니다. ELBO는 다음과 같이 다시 쓸 수 있습니다.

$$\begin{array}{ll} -E_{Q_\theta (Z\vert x)}[\log q_\phi(Z\vert x)] + E_{Q_\theta (Z\vert x)}[\log p_\theta(z,x) &= -\sum_z \log q_\phi(z\vert x) q_\phi (z\vert x) + \sum_z \log p_\theta (z,x) q_\phi (z\vert x)\\ &= \sum_z \left\{-\log q_\phi(z\vert x) + \log p_\theta(z,x)\right\} q_\phi (z\vert x)\\ &= \sum_z \left(\log p_\theta(x\vert z) -\log \frac{q_\phi(z\vert x)}{p(z)} \right) q_\phi (z\vert x)\\ &= \underbrace{-D_{KL}(Q_\phi(Z\vert x)\vert \vert P(Z))}_{(1)} + \underbrace{E_{Q_\phi(Z\vert x)} \log p_\theta(x\vert Z)}_{(2)} \end{array}$$

마지막 줄에 VAE의 목적함수가 나타나 있습니다. 이 목적함수를 해석하자면, (1)번 부분은 Latent space에서 확률변수 $Z$의 사전분포와 데이터 포인트 $x$가 주어진 조건 하에 mapping된 확률변수 $Q(Z\vert x)$의 KL divergence이며, 그 두 분포의 차이를 줄이는 방향으로 학습을 합니다. (2)번 부분은 주어진 잠재변수의 실현값, $z$로부터 encoder 신경망에 의해서 생성된 이미지의 로그 우도함수를 크게 하는 방향으로 학습을 합니다.

실제 (1)번 항에 해당하는 실제 목적함수는 어떻게 구할 수 있을까요? 위에서도 언급했지만, 논문에서는 $N(0, \boldsymbol I)$라는 사전분포를 가정합니다. 위의 notation에서는 $P(Z)$입니다. 이에 대해 사후 확률분포는 다음과 같이 가정하였습니다.

$$Q_\phi(Z\vert x) \sim N(\mu_x, \Sigma_x)$$

위의 표현에서 $\mu_x$와 $\Sigma_x$는 모두 원래의 데이터 $x$를 입력값으로 받는 신경망에 의해 결정됩니다. 이렇게 가정하면 (1)번 항은 결국 $D_{KL}(N(\mu_x, \Sigma_x) \vert \vert N(\boldsymbol 0, \boldsymbol I))$가 됩니다. 두 분포 모두 차원은 같습니다.

$$D_{KL}(Q_\phi(Z\vert x)\vert \vert P(Z)) = D_{KL}(N(\mu_x, \Sigma_x) \vert \vert N(\boldsymbol 0, \boldsymbol I)) = \frac 1 2 \left\{tr(\Sigma_x) + \mu_x\Sigma_x^{-1}\mu_x - K - \log(\vert \Sigma_x\vert )\right\}$$

두번 째 항은 원래 데이터와 잠재변수로부터 decoder를 거쳐 생성된 데이터를 비교합니다. 이 부분을 reconstruction 부분이라고 하는데요, 실제 공간에서도 좋은 성능을 발휘할 수 있도록 하는 역할을 합니다.

두번 째 항에는 두가지 문제점이 있습니다. 첫번째 이유는 두번째 항은 $X =x$일 때, 잠재 확률변수 $Z$의 조건부 기대값을 포함하고 있습니다. 잠재변수 공간이 원래 데이터 공간보다 훨씬 작은 공간이기는 하지만, 기대값을 구하기 위해서는 여전히 상당히 많은 수의 잠재변수의 샘플이 필요합니다. 기대값의 추정에 있어서는 1개의 표본이 그 기대값을 대표한다고 생각합니다. 사실 데이터가 1개 밖에 없을 경우, 그 데이터가 바로 가장 좋은 기대값의 추정치가 됩니다. 이런 논리로, 샘플보통 한 배치를 학습할 때 여러개의 데이터가 들어가므로, 그 데이터의 복원된 이미지를 평균을 내면, 이 평균이 두번째 항에 있는 기대값을 잘 추정해주기를 바라면서 해결합니다.

더 큰 문제는 back propagation 과정에서 발생합니다. 이 문제는 reparameterization trick으로 해결할 수 있습니다.

Repameterization trick

학습할 때, 데이터를 입력하여, encoder 신경망을 거치고 나면, 그 결과물로 잠재변수 공간에서 해당 데이터가 가지는 분포의 평균과 분산을 얻습니다. 이 평균과 분산을 지니는 분포로부터 얻은 임의의 난수를 decoder 신경망을 거치면, 원래 입력 데이터와 비슷한 형태의 데이터를 얻을 수 있다는 것이 VAE의 학습 알고리즘입니다. 원래 입력 데이터와 재현된 데이터를 비교해서 그 차이를 줄이는 방향으로 학습을 하게 됩니다.

이러한 학습의 전제는 결국 decoder 신경망에서 얻어진 복원된 데이터와 원래 데이터의 차이가 encoder 신경망까지 계속 전달되어야 함을 의미합니다. 하지만, encoder 신경망에서 decoder 신경망으로 넘어갈 때, 난수를 생성하는 과정에서 문제가 발생합니다. 난수는 더이상 encoder 신경망으로부터 얻은 평균과 분산의 함수가 아니기 때문입니다. 그래서 VAE에서는 decoder 신경망의 input으로 들어가는 난수를 다음과 같이 표현합니다.

$$z = \mu + u\times \sigma, \quad u \sim N(0, \boldsymbol I)$$

위와 같이 정의하고 나면, 비로소 decoder 신경망의 input으로부터 encoder 신경망의 output으로 연결되는 부분에서 오차 정보를 넘길 수 있게 됩니다. 원 논문에서는 다음과 같은 그림으로 표현합니다.

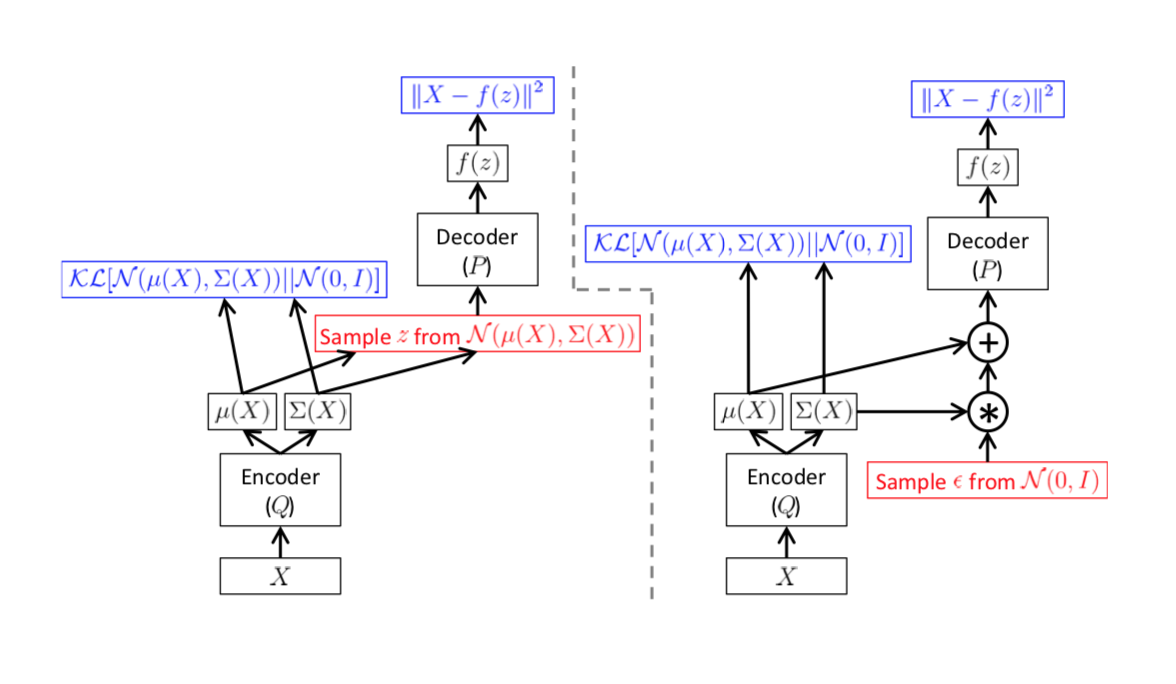
VAE는 거의 최초로 reconstruction이라는 개념을 소개한 방법론입니다. 이후 잇따라 개발된 GAN 모형들과 여러가지 vision 관련된 모형들은 reconstruction이라는 개념을 사용합니다.

마치며

다음 글에서는 VAE를 요약하고 GAN과 비교해서 장점과 단점을 알아보도록 하겠습니다.

kion.kim's profile image

kion.kim

2018-05-30 17:00

Read more posts by this author