시작하며
이제 데이터 분석을 하는 사람이라면 누구나 한번쯤은 들어봤을 CNN일 겁니다. 아래와 같은 구조들로, 주로 이미지 분석에 사용된다고 하나 마케팅 자료분석에서는 시계열에도 활용할 수 있다고 하죠.
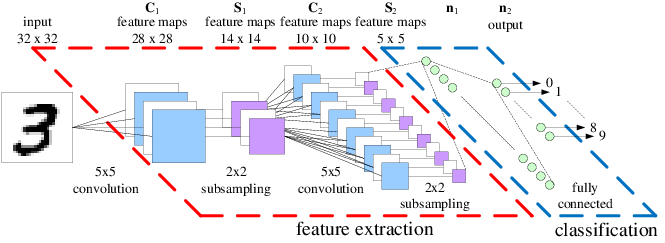
이렇게 유명한 CNN을 DNN과 구분 짓는 가장 큰 요소는 아무래도 convolution입니다. 위의 그림에서는 가장 input에 가까운 쪽에 위치하고 있네요. Convolution은 데이터의 위치적인 특성 을 유지하고, 그게 이미지라면 그림을 구성하고 있는 요소 들을 잘 뽑아낼 수 있다는 장점이 있습니다. 거기다, 단순 DNN에 비해 모수의 숫자를 많이 줄일 수 있는 방법이기도 합니다. 여러분은 컨볼루션에 대해서 알고 있다고 생각하십니까? 혹시 그렇지 않다면, 이 블로그를 통해 컨볼루션에 대해서 자세히 알아보도록 하죠. 먼저 이 글에서는 다음의 내용들을 다룰 겁니다.
- 컨볼루션
- 전치 컨볼루션
- diliated 컨볼루션
이렇게 세가지에 대해서 정확히 알면 아직까지는 컨볼루션을 제대로 이해하는 데 큰 어려움은 없어보입니다. 영어가 편하신 분들은 deeplearning.net에서 정독을 하시면 되겠습니다만, 영어가 마뜩지 않지만 나름 정확한 이해를 원하신다면 이 글이 도움이 될 거라고 믿습니다. 이제 시작해 보죠.
Convolution arithmetic
Cnovolution을 하는 도구가 바로 커널(kernel), 혹은 필터(filter)입니다. 그 커널은 데이터로부터 어떤 성질을 뽑아낼지를 결정합니다.
NOTE: CNN에서는 데이터로부터 커널을 학습시키는데요. 딥러닝이 나오기 전에는 컨볼루션 필터를 영상 전문가가 만들어져서 넣어줬더랬습니다. 전문가가 뽑아내고 싶은 성질을 뽑아주는 일종의 편광필터처럼 사용한 것이죠. 그래서 이름이 필터였습니다. CNN에서도 데이터를 통해 학습된 커널은 필터 역할을 합니다.
Convolution 연산이 어떻게 이루어지는지를 정리해 놓은 블로그들이 많습니다. 그리고 그 블로그들에는 다음과 같은 그림이 언제나 있습니다.
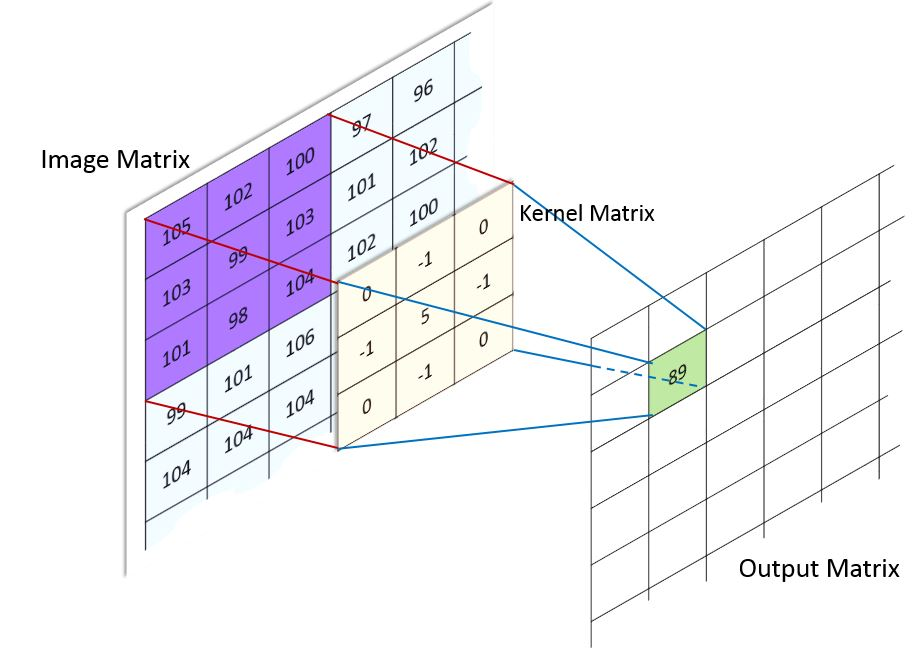
대동소이하지만 위와 같은 그림은 많이 찾아볼 수 있습니다. 여러 그림들 중 가장 직관적인 것 같아서 넣어봤습니다. 커널을 2차원 데이터(주로 이미지겠죠.)에 적용시키면, 결과물로 차원이 다른 이미지가 생성이 됩니다. 가장 쉬운 예가 다음의 그림에 나와 있습니다.
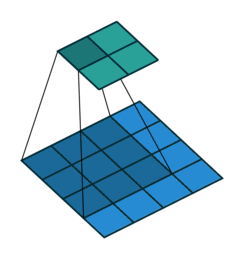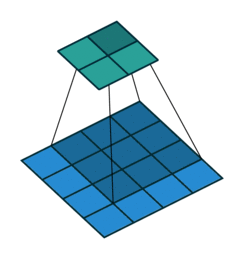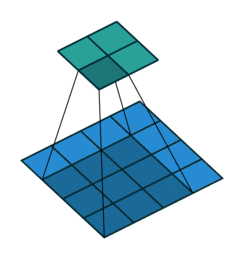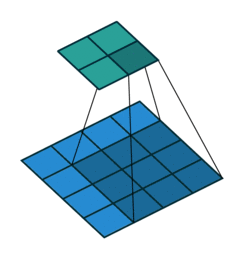
위에는 크기가 가로 세로 3인 커널을, 크기가 4인 이미지에 적용시킨 경우를 의미합니다. 그리고 이 커널을 옆으로 1칸씩 움직이면서, 커널을 반복해서 적용하면 결과물로 가로 세로 2인 이미지를 얻게 됩니다. 많은 블로그나 글들이 여기까지만 설명을 해두었더라구요. 이렇게 하면 커널에 대해서 이해한 것처럼 많은 분들이 생각하고 넘어가십니다. 저 또한 마찬가지로 그랬습니다. 별거 없군!! 하지만, 실제 코드를 짜다 보면 과연 내가 컨볼루션을 이해하고 있나 싶은 회의감이 들죠. 거기다 최근에 많이 쓰이고 있는 커널 트릭들을 보면 돌아버립니다.

그래서 다시 공부를 시작했습니다. 하지만, 쉬운 예를 설명해놓은 것 이외의 조금 복잡한 내용은 찾아볼 수가 없었습니다. 국경을 넘나들며 이런 저런 지루하고 긴 글들을 참조하면 이해할 수 있습니다. 이 글도 지루하지 않다고는 말할 수 없지만, 제가 보기에는 훨~~씬 시간과 공을 들여야 이해할 수 있는 수준이었습니다. 관련 링크는 글의 마지막 부분에 참고문헌으로 걸어두겠습니다.
가장 먼저 알 수 있는 것은 커널을 적용하기 전의 입력과 적용한 후의 출력에는 크게 4가지 변수가 작용합니다.
- 원본 이미지 크기
- 커널의 크기
- stride
- zero padding
용어부터 살펴 보면, 먼저 stride는 커널을 얼마의 간격으로 움직일지를 나타내는 변수입니다. stride가 1이면, 위의 애니메이션처럼 커널을 1칸씩 순차적으로 움직이면서 커널을 적용하고, stride가 2이면 한칸씩 건너 뛰고 커널을 적용합니다. 기본적으로는 stride가 2인 경우는 그림이 반으로 줄어들게 됩니다. 그림의 가로와 세로가 홀수개의 pixel인 경우에는 정확히 반은 아니겠군요. 자세한 내용은 아래에서 하나씩 하나씩 계산해 보겠습니다.
zero padding은 이미지의 외부에 얼마나 많은 pixel을 0으로 채워넣을 것인지를 결정하는 숫자입니다. 다시 말하면, 실제 이미지에는 존재하지 않지만, 0으로 차 있는 이미지의 일부라고 생각을 한다는 것입니다. 실제 이미지보다 더 큰 이미지를 고려한다고 생각하시면 되겠습니다.
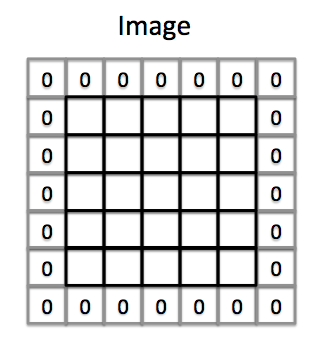
위의 그림은 zero-padding이 1인 상황으로, 그림 밖에 각각 값이 0인 1개의 pixel을 더한다고 의미입니다. 커널을 적용시킬 때에는 원래 이미지가 아닐, 이미지 밖에 있는 값이 0인 픽셀부터 커널을 적용하기 시작합니다.
위에서 보여드린 애니메이션에서는 stride가 1이고 zero-padding이 0일 것입니다. stride가 1인 경우를 unit stride라고도 합니다.
NOTE: 용어가 별로 안중요한 것 같지만, 알아두셔야 합니다. 용어 때문에 한참을 헤메기도 하기 때문이죠.
이렇게 간단한 경우는 너무 쉽게 컨볼루션을 이해할 수 있지만, zero padding이 들어가고 stride가 1이 아니게 되면서 여러가지 경우의 수가 생기게 됩니다.
가장 기본적인 공식
많은 분들이 수식을 좋아하지 않으시는 걸 알지만, 데이터 분석가는 그러면 안되겠죠. 수식은 아이디어를 가장 정확하게 표현할 수 있는 언어와 같은 것입니다. 차원을 계산하는 방법을 수식으로 표현해 보겠습니다. 그렇게 하기 위해서는 먼저 위의 5가지 변수들을 수식에서 쓸 수 있는 기호로 표시해야 겠습니다.
| 의미 | 기호 |
|---|---|
| 원본 이미지 크기 | $i$ |
| 결과물 이미지 크기 | $o$ |
| 커널 크기 | $k$ |
| stride | $s$ |
| zero-padding | $p$ |
가장 먼저 위의 애니메이션과 같은 상황을 표현해 보면, $i = 4$, $o = 2$, $k = 3$, $s = 1$, $p = 0$이 됩니다. 위의 상황을 일반화시키면 다음과 같이 표현할 수 있습니다.
실제 하나하나 대입해서 검산해 보면 같은 2라는 결과를 얻을 수 있습니다. 여기에서는 위의 식이면 충분합니다.
zero-padding이 있는 경우
기본적으로 zero-padding은 양쪽에 들어갑니다. 그러므로 우리가 움직일 수 있는 커널의 범위는 상하좌우로 $p$만큰 더 늘어나게 됩니다. 이를 수식으로 나타내면 다음과 같습니다.
다음은 stride는 1이지만, padding이 있는 경우의 예입니다.
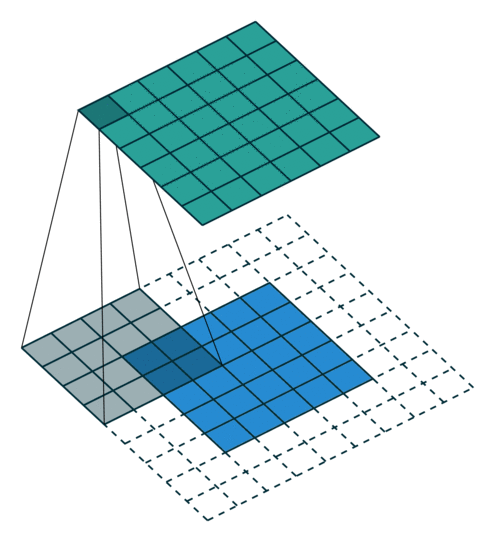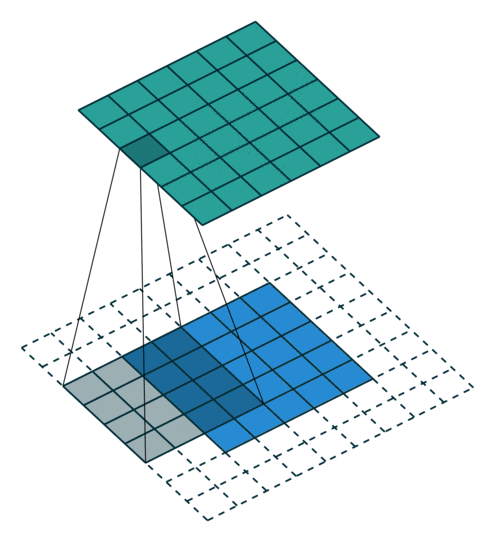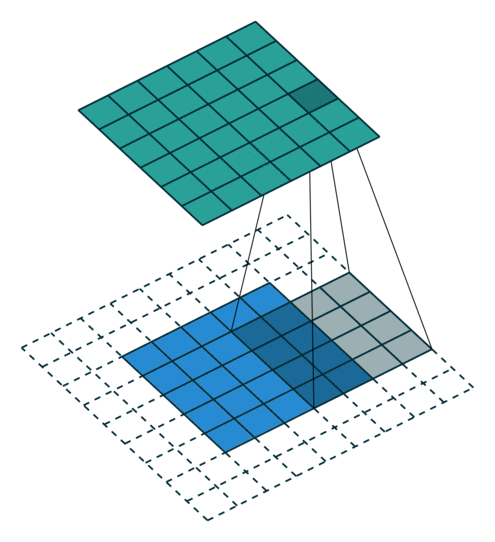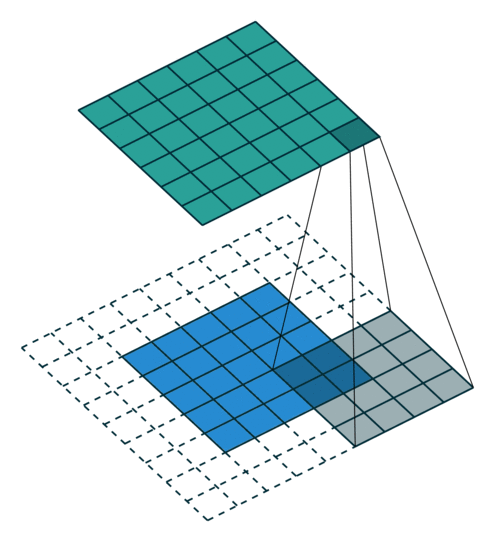
위의 경우에는 zero-padding이 2인 경우입니다.
두가지 zero-padding의 용어를 생각해보면, 두가지 special case가 있습니다. 보통 커널을 통과하면 이미지의 크기가 주로 작아져 있고, 가끔 커지기도 하는데, 만약 크기를 입력 전과 후가 같도록 하고 싶다면 어떻게 할까요? 결국 다른 조건이 동일하다면, zero-padding으로 해결해야 할 것입니다. 이렇게 입력과 출력이 동일하도록 만들어주는 zero-padding을 half padding 이라고 합니다. 그냥 누군가가 명명한 이름일 뿐이지만, 처음에 몰랐을 때는 당황했더랬습니다. 근데 왜 half padding이죠? 여전히 모르겠습니다.
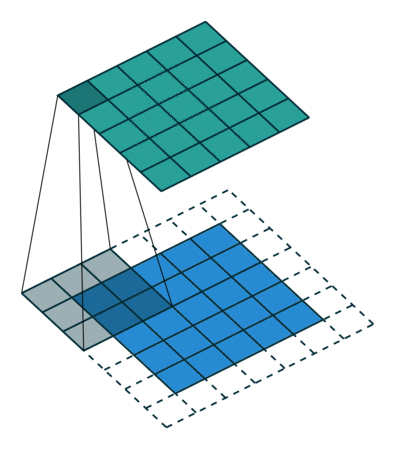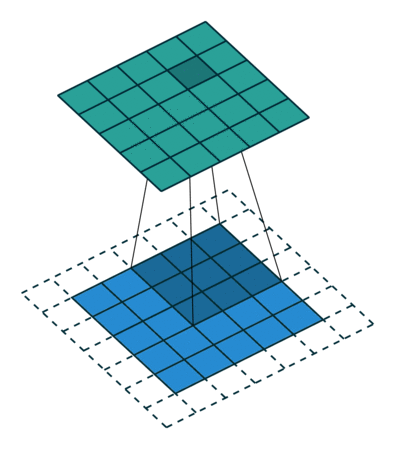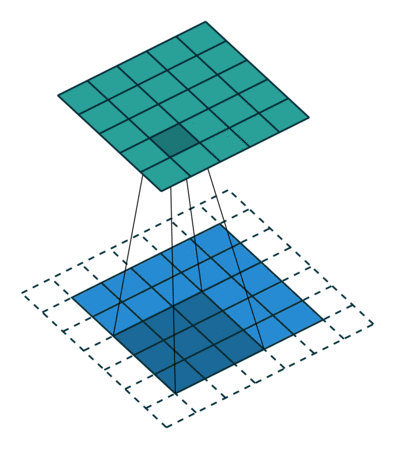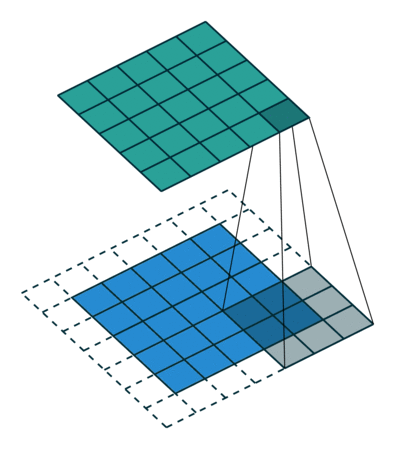
그렇다면, 의미있는 가장 큰 zero-padding은 무엇인가요? 결국 최소 1개의 픽셀이라도 커널에 걸리도록 padding을 주면 될 것입니다. 이렇게 줄 수 있는 한 가장 많은 padding을 부여하라는 것을 full-padding 이라고 합니다. 그나마 이 용어는 직관적으로 이해가 되네요. 아래는 full padding의 예가 있습니다.
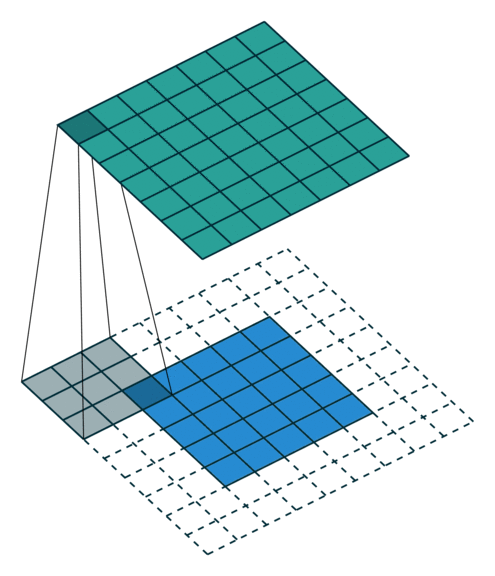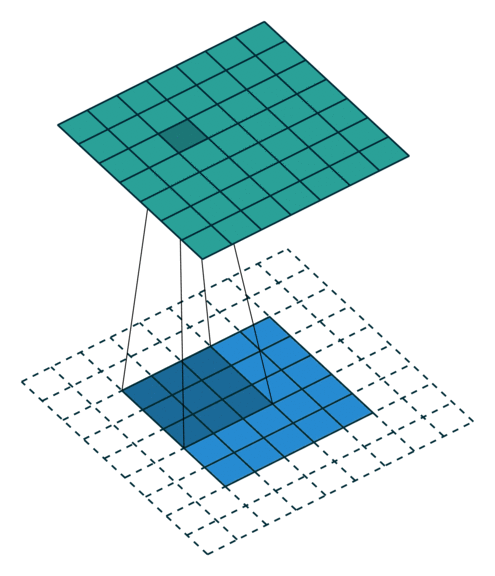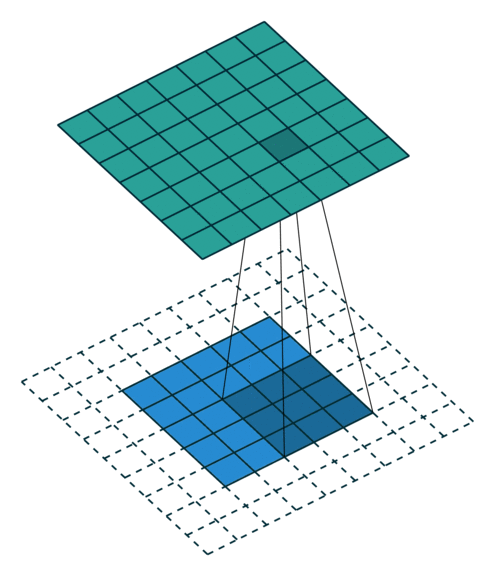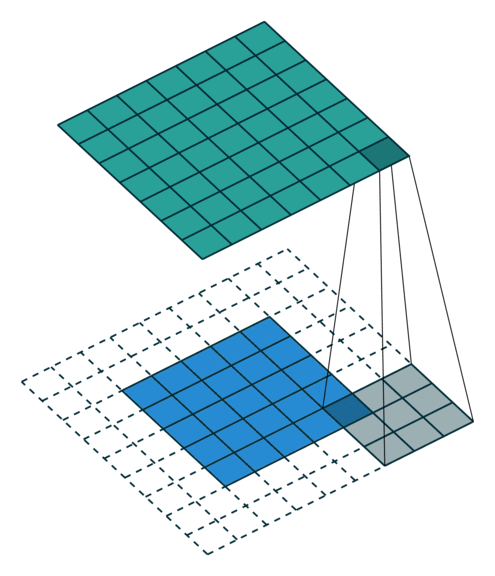
만약 stride가 2라면 어떻게 될까요?
stride가 2인 경우
stride가 2라는 말은 결국 커널을 한칸씩 띄워가면서 적용한다는 것입니다. 만약 stride가 3이면 커널을 두칸씩 띄우게 되겠죠. 가장 간단한 예가 아래에 나와 있습니다. 위의 예제와는 다르게 이제 입력되는 이미지의 크기가 5입니다.
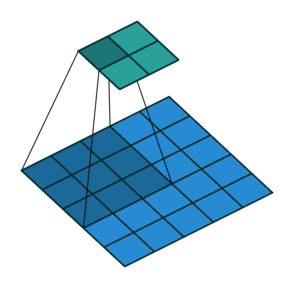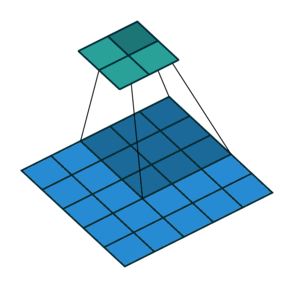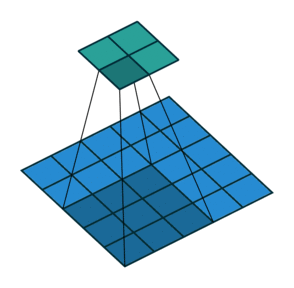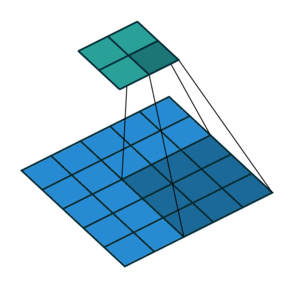
먼 위의 식을 약간만 수정해 보면,
이고 여기에 숫자를 대입해보면 벌써, 1.5라는 수를 얻습니다. 이를 고려해서 좀더 일반화하면 stride를 2라고 hard coding 하지 않고 변수화 시키면,
과 같이 될 겁니다. 하지만, 여기서부터 문제가 되는 건 $s$가 짝수냐 홀수냐에 따라 output의 크기가 달라진다는 것입니다. 만약 stride가 3이면 어떻게 되나요? 벌써 $1\frac 2 3$이라는 이상한 결과가 나오기 시작합니다. 그래서 올림을 취하게 됩니다.
stride가 3인 경우에는 1이 결과물의 dimension입니다. 이 식에 따라 나온 왼쪽 윗부분부터 커널을 stride만큼 움직이면서 오른쪽 아래 방향으로 내려오다가, 커널 크기보다 작은 수의 픽셀이 남으면 그냥 과감히 버리면 됩니다.
이제서야 stride가 무엇이든 상관없이 적용할 수 있는 식이 나왔습니다.
전치 컨볼루션d
과거에는 Deconvolution이라고 불렸습니다. 왠지 컨볼루션의 반대라는 의미를 표현하기 위함인데, 디컨볼루션은 이미 전혀 다른 의미로 공학과 수학에서 사용하고 있기 때문입니다. 그러나 deconvolution이라는 말도 그렇게 쉽게 와 닿지는 않습니다. 컨볼루션은 행렬을 좀 다르게 정의함으로써 행렬 곱으로 표시할 수 있습니다. 먼저 $3\times 3$의 이미지가 있다고 하면, 이 이미지를 $9\times 1$ 벡터로 표현을 할 수 있습니다. 그리고, $2 \times 2$ 커널이 있다고 할 때 다음과 같이 $4\times 9$ 행렬인 $W$를 구할 수 있습니다.
다음과 같이 출력 벡터를 얻습니다.
Convolution이 $3\times 3$ 행렬을 $2\times 2$ 행렬로 바꾸는 역할이라면, 전치 컨볼루션는 그 반대로 작은 차원의 행렬을 큰 차원의 행렬로 바꾸는 연산입니다. $2\times 2$ 행렬을 $4 \times 1$ 벡터로 전환한 후 $W^T$를 곱하면 $9\times 1$차원의 벡터를 얻게 되는거죠.
이렇게 얻은 $\tilde X$를 $3\times 3$ 행렬로 reshape하면 원하는 결과를 얻습니다.
Convolution이 여러개의 픽셀에 있는 정보를 하나의 픽셀로 줄이는 역할을 합니다. Many to one 함수라고 볼 수 있습니다. 반대로 Convolution transponse는 하나의 픽셀 값을 여러개의 픽셀에 뿌려야 합니다. One to many 함수입니다. 위와 같이 $W^T$를 구하는 것 외에 실제로 그러한 함수를 구하는 건 생각보다 직관적이지 않습니다. 그래서 이런 아이디어를 차용하게 된 것일 것입니다.
저런 연결성을 다시 위의 그림과 같은 형태로 표현하면 다음과 같습니다.
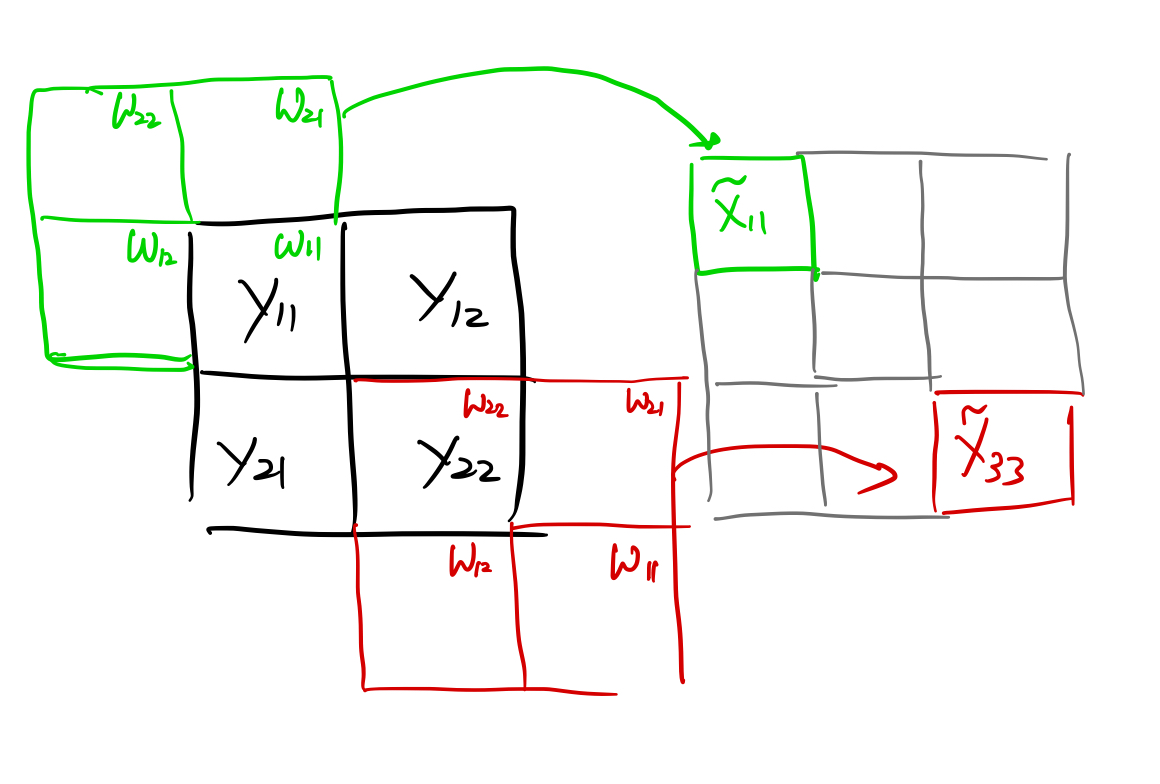
원래의 커널을 뒤집어 놓은 $2\times 2$ 커널을 입력 이미지인 $y$에 zero-padding을 1로 준 상태에서 unit stride로 컨볼루션을 적용한 것입니다. 커널이 뒤집어지기는 했지만, 원래 사이즈의 커널과 stride로 $3\times 3$ 이미지를 복원할 수 있었습니다. zero-padding은 입력과 출력의 크기를 맞춰주기 위해 임의로 설정된 것입니다. 출력의 크기를 $3 \times 3$을 만들기 위해서는 zero-padding이 1이 필요했습니다. 그 이상의 의미는 없습니다.
커널이 뒤집어 지는 것은 상관없습니다. 어차피 데이터에서 추정을 해야 하는 부분이니까요. 여기에서 중요한 것은 입력과 출력의 연결성 입니다.
만약 stride가 2라면 어떻게 될까요? 위에서 본 $W$를 다시 정의해야겠죠. 위읭 예에서는 stride가 2인 상황을 표현할 수 없습니다. stride가 2인 경우에 컨볼루션의 결과물의 사이즈는 1이기 때문입니다. 이 경우 이미지의 가장 왼쪽 윗 픽셀부터 커널 크기만큼 $2 \times 2$만 값을 가지고 나머지 값은 0을 가지는 출력만 내게 됩니다.
커널이 3이고, stride가 2인 상태에서, 입력이미지가 $2\times 2$인 경우에, 출력 이미지의 크기가 $5\times 5$가 되도록 하려면 다음의 그림과 같은 상황이 벌어집니다.
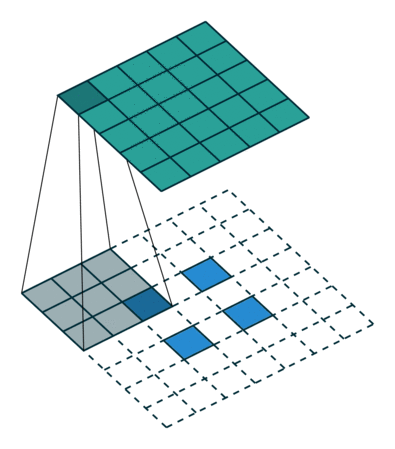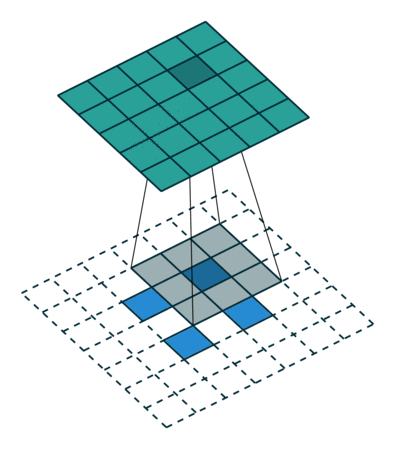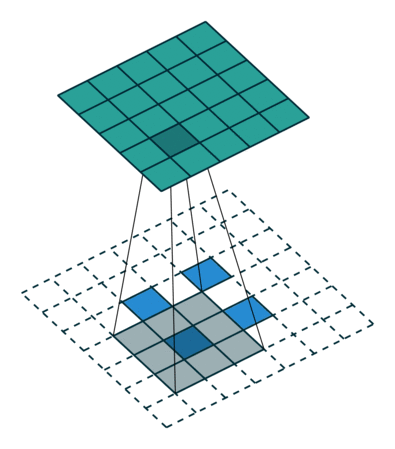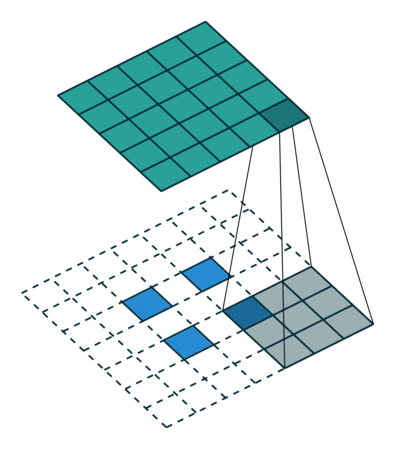
원래의 이미지 사이를 stride 간격만큼 띄우고, 거기에 $3\times 3$ 커널을 unit stride로 적용시킨 것입니다. 그리고 출력 이미지의 크기를 $5\times 5$로 만들어 내기 위해서는 zero-padding이 2가 되어야 했습니다.
위와 같이 전치 컨볼루션를 이미지처럼 표현한 것은 이해를 돕기 위함이지, 계산에서는 저렇게 하지 않습니다. 이미 그림을 봐서 아시겠지만, 훨씬더 넓은 영역(zero-padding을 많이 했기 때문입니다.)에 대해 더욱 촘촘하게(컨볼루션 방향으로는 stride가 2였지만, 전치 컨볼루션 방향으로는 stride가 1입니다.) 컨볼루션을 진행해야 합니다. 행렬, $W$,의 크기가 $25\times 49$로 훨씬 커질 수 밖에 없는데, Convolution 방향의 $W$ 행렬은 $4\times 25$ 밖에 안됩니다. 거의 대부분이 0일 뿐인데 사이즈만 커서 쓸데 없는 계산만 많이 하게 되는거죠.
Parameterization
그렇다면 gluon에서는 전치 컨볼루션를 어떻게 parameter로 정할까요? 결론부터 말하자면, 컨볼루션 방향의 모수들($k,p,s$)을 설정해야 합니다.
예를 들어, $3\times 3$ 커널을 적용시켜서, $2\times 2$에서 $4\times 4$로 가는 전치 컨볼루션를 구하려면, $4\times 4$에서 $2\times 2$로 가는 컨볼루션의 모수들을 다음처럼 함수에 인수로 넣어주어야 합니다. 채널은 간단하게 1이라고 하겠습니다.
nn.Conv2DTranspose(channels = 1, kernel_size = 3, strides = 1, padding = 0, output_padding = 0, dilation = 1)
위의 모수는 다음의 컨볼루션의 모수와 같습니다.
위와 같이 인수를 설정했을 때, $2\times 2$ 크기의 입력을 $4\times 4$ 크기의 출력으로 보낼 수 있습니다.
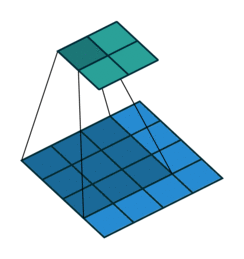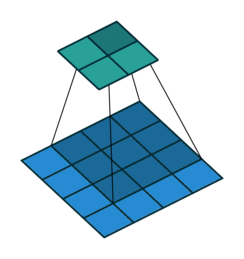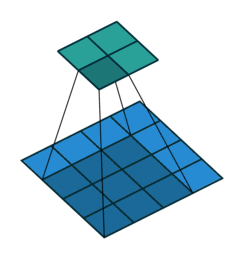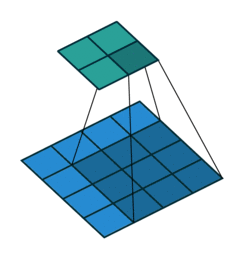
수식으로는 다음과 같이 나타낼 수 있습니다. 입력의 크기를 $i$라고 하고, 출력의 크기를 $o$라고 하면,
$p_o$는 처음 소개되는 모수입니다. 전치 컨볼루션의 입력에 padding이 있을 때 사용합니다. 전치 컨볼루션의 입력에 zero-padding이 있다면, 컨볼루션 입장에서는 출력에 zero-padding이 되어 있다는 이야이겠죠.
dilation
dilation은 truos 알고리즘으로도 알려져 있습니다. 커널을 구성함에 있어서 커널의 픽셀 사이에 얼마나 빈 공간을 줄 것인가를 결정합니다. 백문이 불여일견. 다음의 그림에 잘 나타나 있습니다.
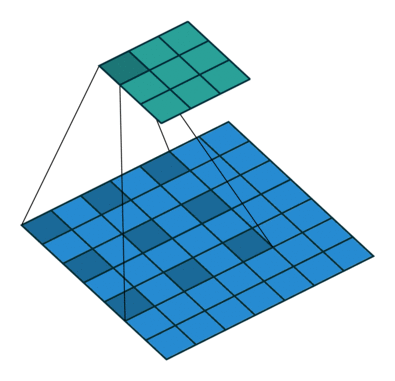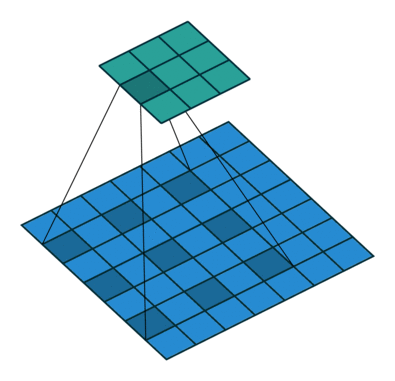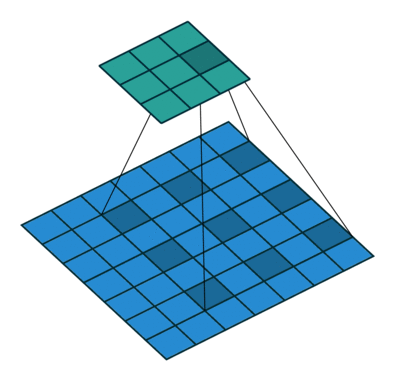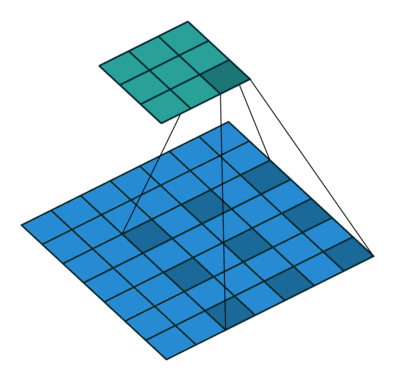
위의 그림은 $i = 7, o = 3, k = 3, dilation = 2, s= 1$인 상황입니다.
일반식은 다음과 같네요.
마치며
생각보다는 호락호락하지 않은 컨볼루션 연산에 대해서 알아보았습니다. 앞으로 보다 많은 형태의 컨볼루션이 나올 수도 있을 것입니다. 이미 이 글에서 다루지 않은 컨볼루션에는 separable 컨볼루션, grouped 컨볼루션이 있네요. 앞으로 이 부분도 공부해서 올리도록 하죠. 이해 안되는 부분이나 틀린 부분 있으면 언제든지 연락주세요.