시작하며
문장을 컴퓨터가 이해할 수 있는 언어로 표현하는 방법에 대해서 계속 이야기 하고 있습니다. 문장을 단어든 문자든 token이라는 최소 단위로 나누고 이들을 어떤 식으로 요약을 해서 하나의 문장으로 요약을 해보자는 것입니다. 그래야만 컴퓨터가 학습을 수행할 수 있을테니까요.
가장 처음에 알아봤던 것은 BoW에 의한 방법입니다. BoW를 word2vec 등의 embedding으로 개선한 것이 CBoW를 사용한 방법들이구요. BoW에서는 token을 one-hot 벡터로 나타내고 이를 단순히 더하거나 평균을 낸 후 이 결과를 machine learning모형에 feeding을 하기만 하면 어느정도 quality의 분석 결과를 보여줍니다. 아주 naive하지만 강력한 방법으로 알려져 있습니다. 적어도 text classification 문제에서는 말입니다.
위의 모형은 그 모형이 문장 자체를 이해한다고 볼 수는 없을 것 같습니다. 그냥 단어가 출현하는 frequency로 패턴을 분류해낸다고 보는 것이 맞겠지요. 문장의 의미를 함축하거나 사람이 문장을 이해하는 과정을 모사하려는 시도는 각각 RNN과 CNN을 이용한 sentence representation에서 이루어집니다. 이에 대해서는 이미 알아보았습니다. 여기에서는 한걸음 더 나아가서, 문장에 속하는 단어 간의 관계를 찾아냄으로써, 문장을 표현하는 Relation Network을 소개하도록 하겠습니다.
Relation network
사실 제가 알기로는 relation network라는 이름은 2017년 Santoro의 논문에서 붙여진 것 같고, 그 개념은 skip-gram이라는 이름으로 이전부터 사용되어 오던 것 같습니다. (아니면 고쳐주시기 바랍니다.)
만약 우리가 $T$개 단어가 포함되어 있는 문장, $S$,에서 $i$ 번째 token인, $t_i$,를 표현하고자 한다고 해보죠. RN에서는 문장에 존재하는 모든 단어 (자기 자신을 포함하지 않으려면, $T-1$개의 단어)들에 대해 그 단어와의 관계를 하나의 벡터로 담는 것입니다. 다음과 같이 두 단어간의 관계를 표현 합니다.
여기서 $U_{left}, U_{right}$와 $W$는 학습해야 할 대상입니다. $\phi$는 non-linear transformation입니다. 또한 $e_i, e_j$는 각각 $i$번째, $j$번째 token을 표현한 embedding입니다.
만약 $T$개의 token을 동일하게 가지고 있는 $N$개의 문장을 포함하고 있는 학습 데이터로 학습을 진행한다고 하면, $N \times \frac {T(T-1)}2 $개의 실질적인 데이터셋으로 학습을 모두 진행한 후에 $U_{left}, U_{right}$와 $W$를 학습하고 난 후에는, sentence representation은 다음과 같이 할 수 있습니다.
모든 pairwise한 단어의 조합$\left(\frac{T(T-1)}2\right)$의 관계를 찾은 다음, 이를 평균을 내는 것입니다.
이렇게 되면, 하나의 문장은 1개의 벡터로 표현되는데 그 크기를 $d$($W$ 행렬의 행의 갯수)라고 하죠.
이 방법은 모든 단어들의 관계를 일정 하게 모두 표현합니다. 이 점이 앞에서 나온 CNN을 이용한 표현 방법과 뒤에서 다루게 될 Self-attention과는 다른 점이고, self-attention은 양 극단인 CNN과 relation network의 절충안이라고 보면 되겠습니다.
알고리즘 핵심 trick
구현의 핵심은 reshape에 있다고 해도 과언이 아닙니다. batch 구조를 유지한 상태에서 모든 token embedding의 조합을 표현해야 하기 때문에 matrix 연산에 많은 공을 들여야 하는 것이 사실입니다.
먼저 위에서 살펴본 $f(t_i, t_j)$ 함수는 다음과 같이 쓸 수 있겠습니다.
개별 inner product의 합이 아니라 $e_i$와 $e_j$를 쌓은 다음 하나의 커다란 행렬 $U = (U_{left}, U_{right})$을 weight값의 모임이라고 보는 것입니다. 엄밀하게 말하면 위의 표현과는 다른 표현이기는 하지만, 계산을 간단하게 할 수 있습니다.
저렇게 표현 하면, 다음과 같이 학습이 이루어집니다.
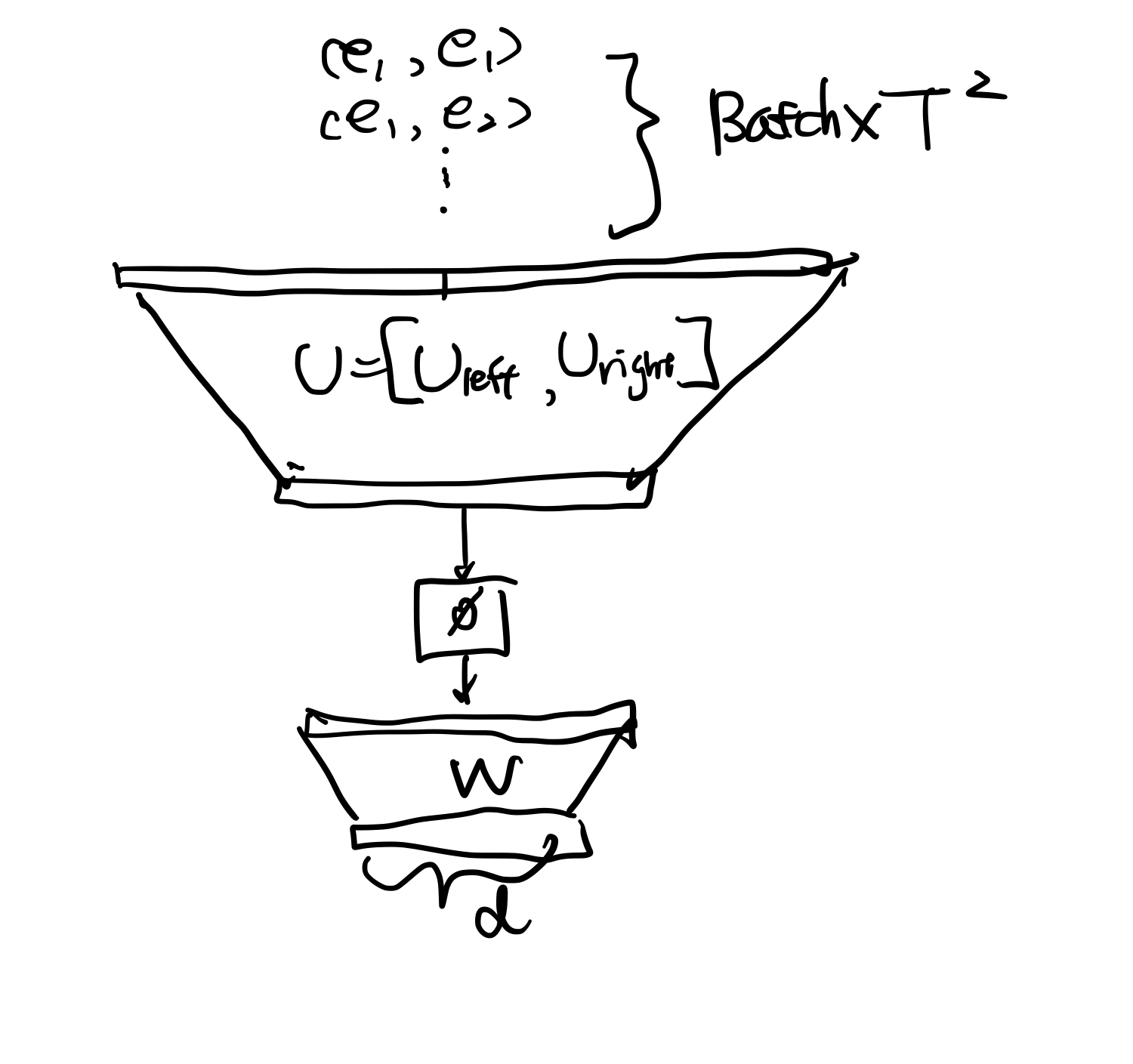
먼저 1개의 배치에 $b$개의 관측치가 있다고 할 때, 더이상 $b$개의 문장형태의 데이터가 들어가는 게 아닙니다. 우리는 하나의 문장에 들어 있는 $T$개의 token의 조합을 모두 고려 합니다. 그리고 그 조합은 각기 출력값에 대한 어떠한 정보를 고려하고 있습니다. 따라서, 우리는 $b \times T^2$의 feature와 answer의 pair를 가지고 있습니다. 그리고 더욱 많아진 데이터를 $U$와 $W$의 신경망에 흘려 backpropagation을 통해 학습을 시키게 되는 것입니다. 그러므로 우리는 하나의 문장에서 $i$ 번째 token과 $j$ 번째 token, $e_i$와 $e_j$,의 모든 조합 $T^2$개의 조합을 독립적인 input 벡터로 만들어주어야 하는데 이 작업을 위해서는 몇가지 trick이 필요합니다.
먼저 하나의 문장은 기본적으로 $T\times N$의 행렬로 표시가 됩니다. (그림에서 $n =T$, $m = N$으로 생각하시면 되겠습니다.) 여기서 $T$는 한 문장 안에 속해 있는 token의 갯수를 $N$은 Token의 차원을 의미합니다. 데이터에 나타나는 총 유의한 단어의 숫자일 수도 있고 단순히 자모일 수도 있습니다. 그리고 하나의 batch에는 mini-batch의 크기만큼의 문장이 들어갈 것입니다. 이 상황을 그림으로 표현하면, $T\times N$ 크기의 사각형이 3개 나열된 형태로 생각할 수 있습니다. 따라서 현재는 $3 \times T \times N$이라는 입력 벡터를 가지고 있는 상황입니다.

여기서 트릭의 시작인데요. 이 행렬을 1차원에 하나의 차원을 더 늘려서 $3 \times 1 \times T \times N$으로 만든 다음에 1차원 방향으로 $T$개 복사를 해서 위 그림의 마지막 줄에 있는 것처럼 복사된 데이터가 가로방향으로 $T$개 쌓아 놓은 $3 \times T \times T \times N$를 만듭니다. 다음은 아래의 그림에서 나타나 있는 과정처럼 세로로 같은 입력이 복사되어 있는 동일한 크기의 데이터를 만들어 놓습니다.
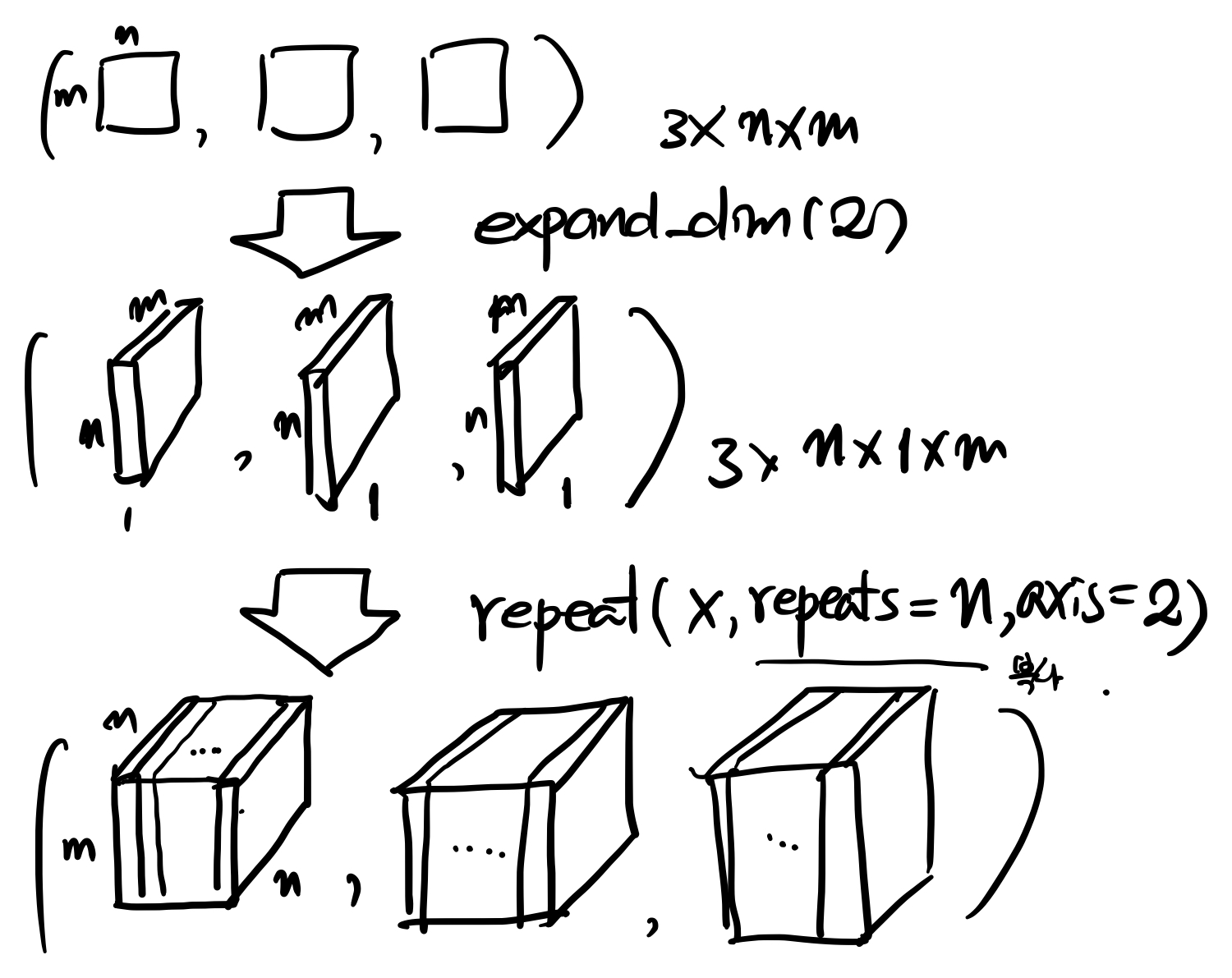
두개의 행렬을 4차원 방향으로 붙이게 되면, mini-batch당 다음과 같은 행렬을 얻을 수 있습니다.
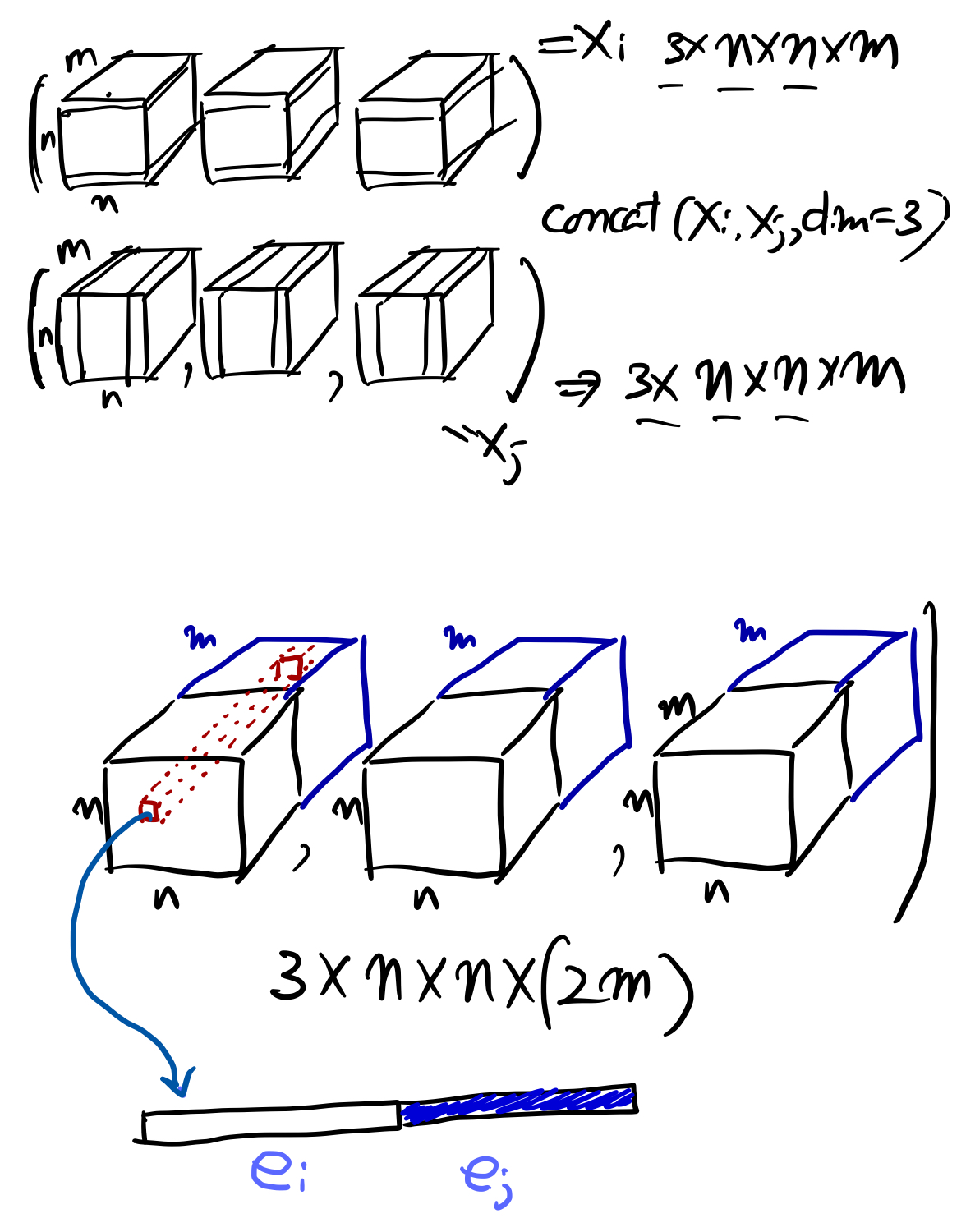
저렇게 놓게 되면, 하나의 데이터에서 보면 $i$ 번째 $j$ 번째에 있는 $2\times N$ 열의 값은 앞의 $m$개 원소에는 $i$ 번째 token의 embedding이고, 뒤의 $m$개의 원소에는 $j$ 번째 token의 embedding이 들어 있게 됩니다. 이제 이렇게 만들어진 데이터를 $T^2$개의 독립적인 데이터로 풀게 되면 최종적으로 $3 \times T^ 2$개의 $2\times m$ 데이터가 새로 생기게 되고 이 것을 모형의 입력으로 사용한다는 것이죠. 이 부분이 relation network의 가장 핵심적인 부분입니다. 이제 이 내용을 코드를 보면서 확인해 보도록 하겠습니다.
Gluon을 이용한 코딩
먼저 모듈을 불러와야 겠습니다. 데이터를 불러와서 Data Iterator를 만드는 과정까지는 앞의 블로그 BoW를 이용한 text-classification를 참고하시기 바랍니다. 여기에서는 실제로 위에서 보여드린 trick이 어떻게 구현되어 있는지를 살펴보도록 하겠습니다.
먼저 코드 전체는 따로 보여드리고, 위에서 언급된 부분이 나와 있는 부분부터 확인해 보겠습니다.
def hybrid_forward(self, F, x):
# (x_i, x_j)의 pair를 만들기
# 64 배치를 가정하면
x_i = x.expand_dims(1) # 64 * 1* 40 * 2000
x_i = F.repeat(x_i,repeats= self.SENTENCE_LENGTH, axis=1) # 64 * 40 * 40 * 2000
x_j = x.expand_dims(2) # 64 * 40 * 1 * 2000
x_j = F.repeat(x_j,repeats= self.SENTENCE_LENGTH, axis=2) # 64 * 40 * 40 * 2000
x_full = F.concat(x_i,x_j,dim=3) # 64 * 40 * 40 * 4000
위의 부분이 $i$번째 $j$번째 embedding을 조작하는 부분입니다. 주석으로 해당 레이어의 크기를 적어두었습니다. 주석은 batch size가 64라고 가정한 차원 계산입니다. 또한 중요한 것이 이 relation network는 아주 큰 네트워크인만큼 메모리 사용량에 신경을 써야 합니다.
# batch*sentence_length*sentence_length개의 batch를 가진 2*VOCABULARY input을 network에 feed
_x = x_full.reshape((-1, 2 * self.VOCABULARY))
_x = self.g_fc1(_x) # (64 * 40 * 40) * 256
_x = self.g_fc3(_x) # (64 * 40 * 40) * 256
_x = self.g_fc4(_x) # (64 * 40 * 40) * 256
위의 부분은 $Vocab \times 2$만큼 커진 벡터를 $N\times T^2$개 만든 후에 4개의 layer를 거칩니다. 그렇게 되면 이제 classifier를 정의해야 할 시점입니다. 그렇게 해서 얻어진 두 단어 간의 관계 정보가 압축되어 있는 hidden 벡터의 크기는 256입니다.
# sentence_length*sentence_length개의 결과값을 모두 합해서 sentence representation으로 나타냄
x_g = _x.reshape((-1, self.SENTENCE_LENGTH * self.SENTENCE_LENGTH,256)) # (64, 40*40, 256) : .1GB
sentence_rep = x_g.sum(1) # (64, 256): ignorable
만약 weight가 결정된 후에 feature map을 얻기 위해서는 token의 모든 조합에 대해 합을 낸다면, 모든 token 간의 관계가 고려된 $d$ 차원의 벡터를 얻게 됩니다. 그 뒤에 따라올 과정은 straightforward 합니다.
아래는 전체 classifier code입니다.
class RN_Classifier(nn.HybridBlock):
def __init__(self, SENTENCE_LENGTH, VOCABULARY, **kwargs):
super(RN_Classifier, self).__init__(**kwargs)
self.SENTENCE_LENGTH = SENTENCE_LENGTH
self.VOCABULARY = VOCABULARY
with self.name_scope():
self.g_fc1 = nn.Dense(256,activation='relu')
self.g_fc2 = nn.Dense(256,activation='relu')
self.g_fc3 = nn.Dense(256,activation='relu')
self.g_fc4 = nn.Dense(256,activation='relu')
self.fc1 = nn.Dense(128, activation = 'relu') # 256 * 128
self.fc2 = nn.Dense(2) # 128 * 2
# 1253632 param : 약 20MB
def hybrid_forward(self, F, x):
# (x_i, x_j)의 pair를 만들기
# 64 배치를 가정하면
x_i = x.expand_dims(1) # 64 * 1* 40 * 2000* : 0.02GB
x_i = F.repeat(x_i,repeats= self.SENTENCE_LENGTH, axis=1) # 64 * 40 * 40 * 2000: 1.52GB
x_j = x.expand_dims(2) # 64 * 40 * 1 * 2000
x_j = F.repeat(x_j,repeats= self.SENTENCE_LENGTH, axis=2) # 64 * 40 * 40 * 2000: 1.52GB
x_full = F.concat(x_i,x_j,dim=3) # 64 * 40 * 40 * 4000: 3.04GB
# batch*sentence_length*sentence_length개의 batch를 가진 2*VOCABULARY input을 network에 feed
_x = x_full.reshape((-1, 2 * self.VOCABULARY))
_x = self.g_fc1(_x) # (64 * 40 * 40) * 256: .1GB 추가메모리는 안먹나?
_x = self.g_fc2(_x) # (64 * 40 * 40) * 256: .1GB (reuse)
_x = self.g_fc3(_x) # (64 * 40 * 40) * 256: .1GB (reuse)
_x = self.g_fc4(_x) # (64 * 40 * 40) * 256: .1GB (reuse)
# sentence_length*sentence_length개의 결과값을 모두 합해서 sentence representation으로 나타냄
x_g = _x.reshape((-1, self.SENTENCE_LENGTH * self.SENTENCE_LENGTH,256)) # (64, 40*40, 256) : .1GB
sentence_rep = x_g.sum(1) # (64, 256): ignorable
# 여기서부터는 classifier
clf = self.fc1(sentence_rep)
clf = self.fc2(clf)
return clf