VAE의 목적
앞의 글에서 이미 말씀드렸지만, 데이터의 분포를 추정함에 있어, VAE의 목표는 두가지라고 할 수 있습니다. 하나는 아주 큰 차원에 존재하는 데이터의 차원을 효과적으로 줄이는 것입니다. manifold hypothesis에 근거하여 VAE에서는 큰 차원의 데이터 공간보다는 훨씬 작은 공간에서 데이터를 표현하고자 합니다. 이렇게 하면 보다 작은 차원에 존재하는 분포만 고려하면되기 때문에 계산도 훨씬 간단해 지는 효과도 있습니다.
다른 하나는, 원래 데이터의 분포의 구조를 유지하는 것입니다. 예를 들면, 784차원의 MNIST 데이터를 2차원으로 줄인다고 할 때, 784차원의 원래 이미지가 가지는 유사도를 그대로 2차원에서도 표현하고 싶은 것입니다. 숫자 ‘1’도 쓰는 사람의 필체에 따라 수많은 형태가 나올 텐데, 그래도 사람이 숫자 2와는 쉽게 구분할 수 있는 것을 보면, 다양한 모양의 ‘1’이라는 숫자는 숫자 ‘2’보다는 더 가까워야 할 것입니다.
Latent space
이런 두가지 목적을 달성하기 위해서 VAE는 잠재변수 $Z$를 도입합니다. 이 잠재변수는 몇 개의 모수로 결정이 되는 샘플 추출이 용이한 확률변수입니다. 관측된 데이터를 확률변수 $X$라고 나타낼 때, 이 확률변수는 원래 데이터가 가지는 $D$ 차원보다는 훨씬 작은 $K$ 차원을 가집니다. 수학적으로는 $ X\in \mathbb R^D, Z\in \mathbb R^K$라고 표현합니다.
우리는 $K$ 차원 공간에서 데이터의 분포를 표현하기를 원합니다. 하지만, 관측된 데이터의 분포와 잠재변수의 분포는 어떤 식으로든 연결이 되어야 합니다. 그래서 우리는 데이터의 확률분포 $X$가 $x$로 주어졌다면, 그 점에 대응하는 값이 확률변수 $Z$가 이루는 공간의 어느 원소, $z$에 해당하는지를 알고 싶습니다. 이런 상황을 수학적으로 나타내면, 결국 우리가 찾고자 하는 것은 $P(Z\vert X)$입니다. Bayesian notation에 빗대면, $P(Z)$는 사전 확률분포 (prior distribution)으로, $P(Z\vert X)$는 사후분포 (posterior distribution)라고 표시할 수 있습니다.
NOTE: Notation에 대해서 설명하자면, 확률변수는 $X$와 $Z$와 같이 대문자로 나타내고, 확률변수의 실현값은 $x$, $z$와 같이 소문자로 나타냅니다. 대문자 $P$와 $Q$는 확률 분포를 나타내고, $p$와 $q$는 확률분포와 대응되는 확률밀도 함수 (probability density function)를 의미합니다. 앞으로 많은 subscription이 보일텐데, 이는 확률분포와 확률밀도함수의 의미를 좀더 명확하게 해주는 의미로 사용됩니다. $P_X$라고 하면 확률변수 $X$의 확률분포를 의미합니다. $p_x$는 $X$의 확률밀도 함수를 의미하고, 조건부 확률분포를 나타내고 싶으면, $P_{X\vert Z}$라고 표현하겠습니다. Subscription도 확률변수를 의미하므로 대문자를 사용하겠습니다. 기대값은 $E$로 표시하고 마찬가지로 의미를 명확하게 하기 위해서는 아래첨자를 씁니다. 아래첨자는 모두 대문자로 표시하고, $E_{X\vert Z}$라고 하면 확률변수 $Z$가 주어졌을 때, 확률변수 $X$의 기대값이고, 이는 확률 변수 $Z$가 어떤 값이 주어지는가에 따라 달라지므로, $Z$의 함수가 됩니다.
VAE는 생성모형입니다. 따라서, 모형을 다 추정하고 난 후에는 모형을 생성할 수 있어야 합니다. 모형을 어떻게 생성할까요? VAE에서는 어떤 정해진 공간에서 숫자들을 뽑아내고, 그 숫자들을 하나의 시작점으로 이미지를 생성해 냅니다. 그럴려면, 어떤 정해진 공간이 필요하고, 그 공간의 틀을 만드는 것이 잠재변수 $Z$가 가지는 확률공간입니다. VAE에서 하는 작업은 그 틀이 최대한 데이터의 분포를 반영하도록 하는 것입니다. 만약 확률변수 $Z$가
라는 2차원 정규분포를 따른다고 하면, $P(Z)$는 다음과 같은 확률분포를 가집니다.

위의 그림에서 보면 숫자 0에서 9까지에 해당하는 숫자들이 아무런 패턴 없이 뿌려져 있는 것을 확인할 수 있습니다. 사전 분포이므로, 실제 데이터와 아무런 관계가 없으니, $Z$가 정의된 2차원 공간에 임의로 흩어져 있습니다.
VAE가 하는 일은 잠재변수의 평면에 의미를 주고자 하는 시도라고 볼 수 있습니다. 아무 의미없는 random noise일 뿐인 $P(Z)$를 연결시켜, $P(Z\vert X)$를 찾되, 그 사후분포는 다음과 같은 모양을 띄기를 원합니다.
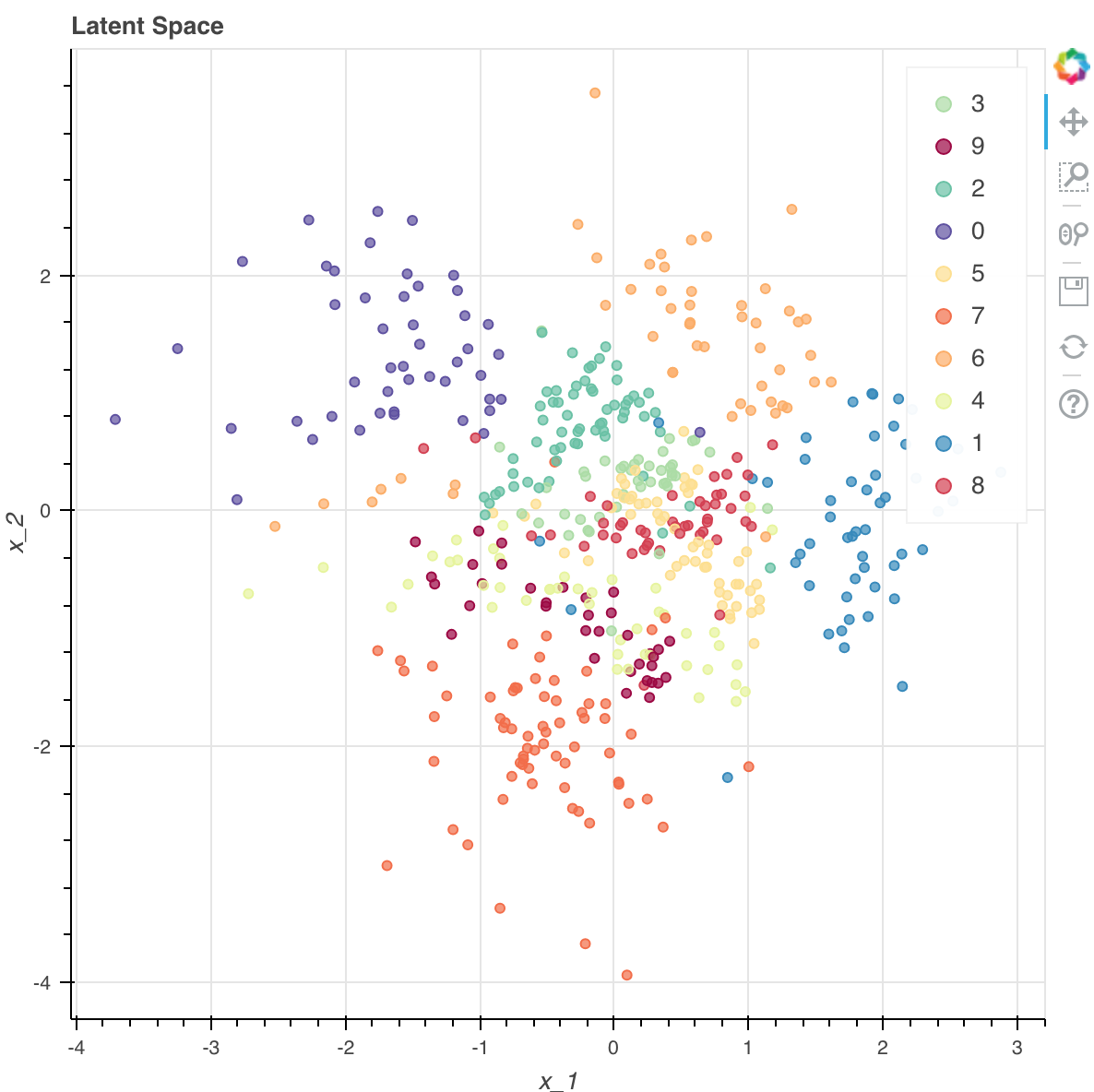
위의 그림은 Encoder 신경망을 학습시키고 난 후에 어떤 MNIST data의 숫자가 2차원 공간에 어떤 식으로 mapping되는지를 보여줍니다. 위와 같이 얻을 수만 있으면, 우리는 새로운 1을 뽑아내려면, 오른쪽 아래에 1이 모여 있는 점 부근에서 새로운 표본을 추출 후 이미지를 만들어내면 될 것입니다. 이미지를 만들어 내기 위해 신경망을 쓰고, 의미 있는 사후분포를 찾기 위해서 또 다른 신경망을 씁니다.
두개의 신경망
확률변수 $X$와 $Z$는 두 개의 신경망(feedforward 신경망)로 연결이 되어 있습니다. $X$에서 $Z$로 변환할 때에는 $D$ 차원의 원래 데이터를 입력으로 받아들여, 잠재변수의 모수를 결과물로 내는 신경망을 통해 연결이 되어 있습니다. 잠재변수의 모수라고 하면, 우리는 정규분포를 가정했으므로, 잠재변수의 평균과 분산이 되겠습니다. 분산도 서로 독립인 정규분포를 가정했으므로, 잠재변수의 차원수만큼의 모수만 출력하면 되겠습니다. 이 신경망을 encoder 신경망이라고 합니다.

반대로 $Z$에서 원래의 데이터로 복원(reconstruct)할 때에는 $K$ 차원의 잠재변수를 입력으로 받아 $D$ 차원의 데이터를 출력으로 하는 신경망을 통해 연결이 되어 있습니다. 이를 decoder 신경망이라고 합니다.
수학적으로 보다 정확하게 표현해 보겠습니다.
잠재변수의 확률변수를 표현할 수 있는 모수의 개수를 $p$개라고 하면, encoder 신경망은 다음과 같이 표현할 수 있습니다. 여기서 $\zeta$는 신경망의 weight값입니다. encoder 신경망을 통해 얻은 모수를 바탕으로 잠재변수는 조건부 분포, $Q(Z\vert x)$를 따른다고 가정합니다. 이 조건부 분포는 여러가지로 가정할 수 있겠지만, 논문에서는 정규분포로 가정을 합니다. 정규분포는 평균과 분산을 모수로 가지므로, 정규분포의 경우 $\psi(x; \zeta)$는 $K$개의 평균값과 $K$개의 분산값, 합해서 $2K$개의 숫자를 출력합니다. 다시 말하면, 이 경우에는 $p= 2K$입니다. 이 모수벡터를 $2K\times 1$ 크기의 $\phi$라고 하면,
로 구성됩니다. 여기서 $\mu(x; \zeta)$와 $\sigma(x; \zeta)$는 각각 $K\times 1$ 차원의 평균과 분산 벡터입니다. 이런 상황에서, 데이터가 주어져 있는 경우 잠재변수의 조건부 분포는 다음과 같이 쓸 수 있습니다.
요약하자면, 원래 데이터를 입력으로 넣으면, encoder 신경망은 잠재변수의 모수를 출력하고, 잠재변수는 이 모수를 평균과 분산으로 하는 조건부 분포를 따름을 의미합니다.
decoder 신경망은 $f(z;\theta):\mathbb R^K \rightarrow \mathbb R^D$로 변환하는 함수로 $\theta$는 신경망의 weight 값들입니다. 이러한 신경망에 근거해서 만약에 잠재변수 $Z=z$가 선택이 되면, 데이터는 $f(z;\theta)$를 중심으로 $\sigma^2 I$를 분산으로 가지는 분포를 따릅니다. 이를 수식으로는 다음과 같이 나타냅니다.
를 따른다고 가정합니다. 여기서 $\sigma^2$는 hyper-parameter로 분석가에 의해 결정이 됩니다.
마치며
다음 글에서는 최우추정법과 variational inference에 대해서 알아보도록 하겠습니다.