GAN과 WGAN 사이

시작하며..

지난 글에서 논의된 내용들을 정리해 보겠습니다. 다시 한번 remind하면, Optimal인 판별기를 가정한 경우의, GAN의 손실함수는

$L(G,D^* ) = 2D_{JS}(p_{data}||p_G) - 2\log 2$

입니다. 개념적으로는 GAN이 생성된 데이터와 원래 데이터 간의 JS 거리를 가장 작게 하는 방향으로 학습이 되고 있다고 할 수 있겠습니다.

하지만, JS 거리가 언제나 잘 정의가 되는 것은 아니었죠. Support를 공유(absolute continuity 가정)해야만 가능한 것으로, manifold hypothesis에 의하면, support를 공유하지 않을 활률이 아주 높다는 것입니다. 그렇다면 좀더 안정적으로 정의되는 분포간의 거리를 재는 measure가 필요한데요, W-거리가 그러한 성질을 만족합니다. W-거리는 비교하는 두 분포 간의 absolute continuity를 요구하지 않는 거리입니다. 대신, 대상이 되는 분포의 absolutely continuity만 요구합니다. 기존의 조건보다 많이 완화된 조건입니다. 거기다, KL/JS divergence가 0으로 수렴하지 않더라도, W-거리는 0으로 수렴할 수 있고, W 거리가 수렴하면, KL/JS divergence는 수렴을 해야만 합니다. 그러니, W를 0으로 만드는 작업이 KL/JS divergence를 0으로 만드는 작업보다 훨씬 쉬울 것 같습니다. 훨씬 안정적으로 정의될 수 있다는 것을 의미합니다.

그래서 W-거리를 구했지만, 이 metric은 원래의 정의에 따르면 거리를 구하는 것만으로도 벅차다는 또다른 난관에 봉착했죠. 이번 글에서는 어떻게 이 문제를 풀어내는지를 살펴 보겠습니다.

Kantorvich - Rubinstein Duality

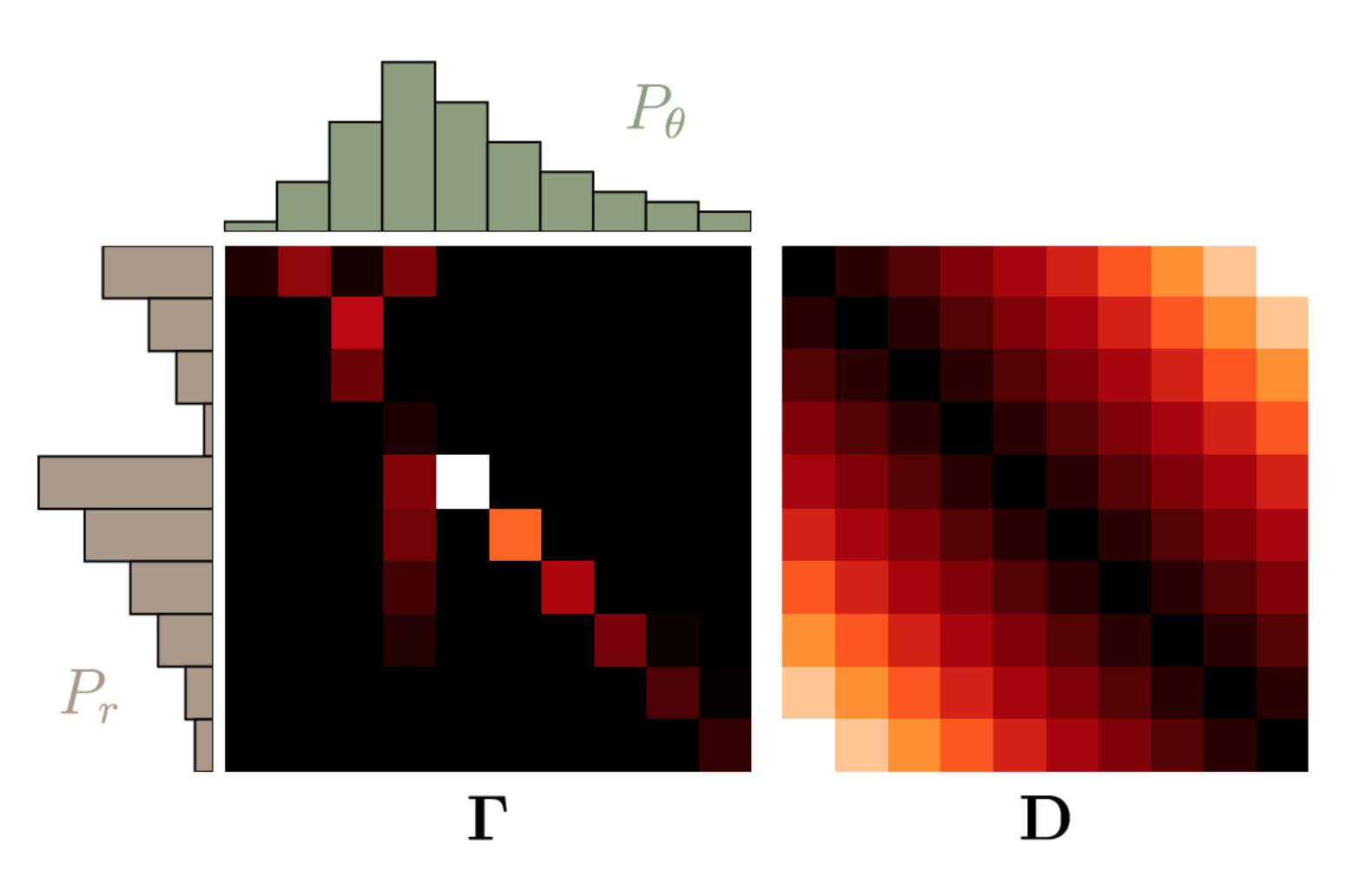
$P_\theta$와 $P_r$을 Discrete한 분포라고 가정하면, $\gamma(x,y)$를 다음과 같은 matrix로 나타낼 수 있습니다.

$\gamma = \left(\begin{array}{ccc} \gamma(x_1, y_1) &\cdots &\gamma(x_1, y_l) \\ \vdots &\cdots & \vdots \\\gamma(x_l, y_1) &\cdots &\gamma(x_l, y_l)\end{array}\right)$

그리고 support의 원소의 거리를 나타내는 matrix, $D$를 다음과 같이 정의하면,

$D = \left(\begin{array}{ccc} \|x_1 - y_1\| &\cdots &\| x_1 - y_l\| \\ \vdots &\cdots & \vdots \\\|x_l - y_1\| &\cdots &\|x_l - y_l\|\end{array}\right)$

위의 두 행렬의 Fabuluous norm으로 기대값을 구할 수 있습니다. $\left<D, \gamma \right>_F = E_{(x, y) \sim \gamma(x, y)} \|X-y\|$

Wasserstein_transportation_example_1

$vec$ operator는 행렬을 벡터로 표현하는 operator입니다. 위의 행렬은 길이가 $l^2$인 벡터들로 바뀝니다.

$d = vec(D), g = vec(\gamma)$

다음의 cost, $c = d^Tg$

를 최소화하고 싶은 목적함수로 하되, 이 최적화 과정에는 다음과 같은 constraint들이 있습니다.

$d$의 모든 원소는 0보다 크다
$\sum_{i=1}^l \gamma(x_i, y) = P_r(y)$
$\sum_{j=1}^l \gamma(x, y_j) = P_\theta(x)$

위의 조건을 표현하기 위해 적절히 design 행렬 $A$를 정의하면,

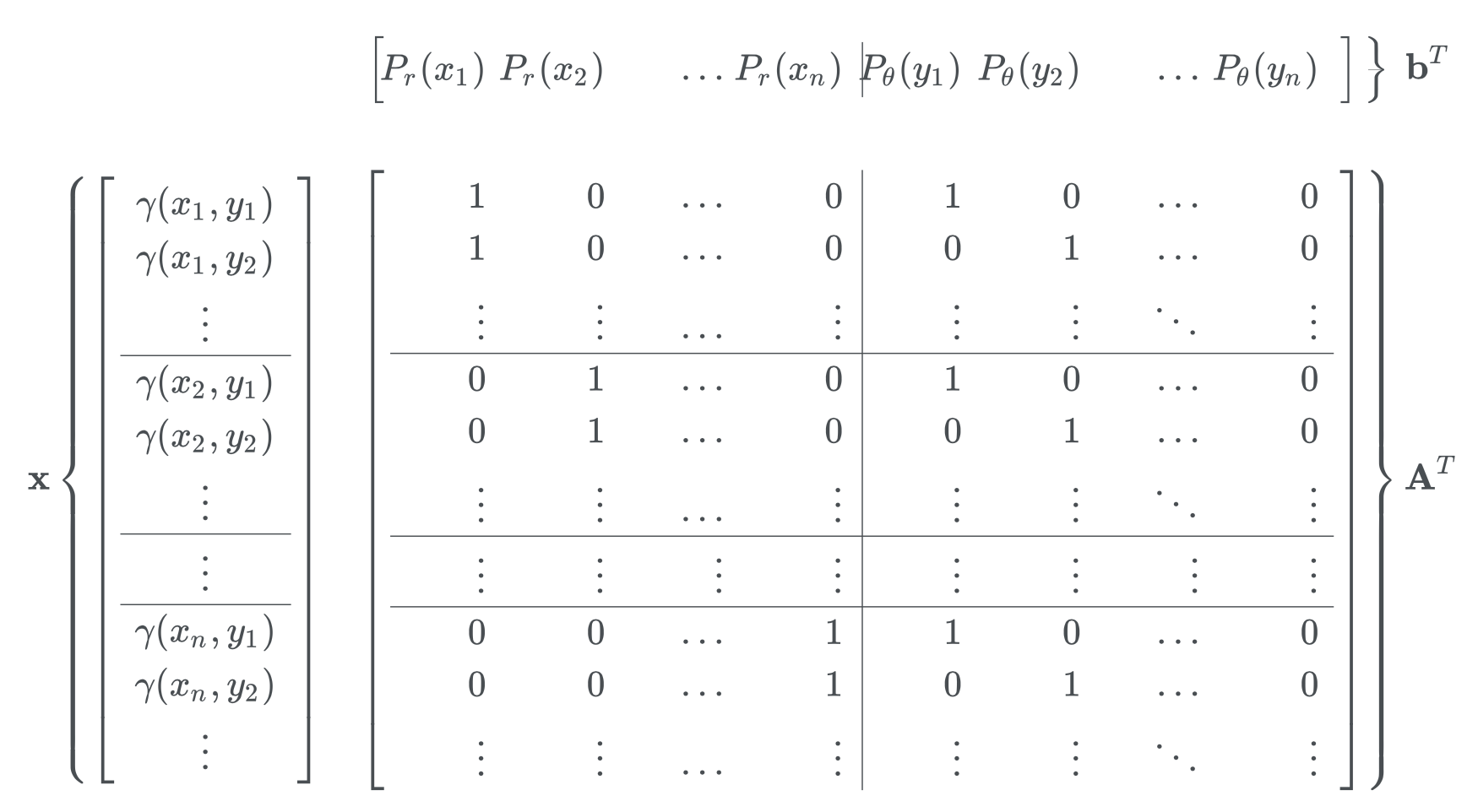
WGAN_KW_Design

위의 조건 중 두번째 세번째 조건은 다음과 같이 쓸 수 있습니다. $A\cdot x = b$

요약하면, EM distance를 구하는 것은 다음의 linear programming 문제를 푸는 것과 같습니다.

$min_{g} c = min_{g} d\cdot g$

s.t. $g \ge 0$ and $Ax = b$

NOTE: 다음은 python으로 moving cost를 최소화한 transportation plan을 찾는 방법을 simulation 해놓은 예제입니다.

import numpy as np
from scipy.optimize import linprog

p_r = (.1, .2, .1, .2, .1, .2, .1)
p_t = (.1, .1, .1, .1, .1, .1, .4)

l = 7
A_r = np.zeros((l,l,l))
A_t = np.zeros((l,l,l))

for i in range(l):
    for j in range(l):
        A_r[i,i,j] = 1
        A_t[i,j,i] = 1  

D = np.zeros((l, l))
for i in range(l):
  for j in range(l):
    D[i, j] = np.abs(i-j)

A = np.concatenate((A_r.reshape((l, l**2)), A_t.reshape((l, l**2))), axis = 0)
b = np.concatenate((p_r, p_t), axis = 0)
c = D.reshape((l**2))

opt_res = linprog(c, A_eq = A, b_eq = b)
emd = opt_res.fun
gamma = opt_res.x.reshape((l, l))

위에서 $\gamma(x,y)$는 최적의 transportation이고 다음은 해당 transportation plan의 결과물입니다.

array([[0.1, 0. , 0. , 0. , 0. , 0. , 0. ],
       [0. , 0.1, 0.1, 0. , 0. , 0. , 0. ],
       [0. , 0. , 0. , 0. , 0. , 0. , 0.1],
       [0. , 0. , 0. , 0.1, 0. , 0.1, 0. ],
       [0. , 0. , 0. , 0. , 0.1, 0. , 0. ],
       [0. , 0. , 0. , 0. , 0. , 0. , 0.2],
       [0. , 0. , 0. , 0. , 0. , 0. , 0.1]])

위의 배열을 가로 세로로 모두 합해 보면, 두 분포를 marginal 분포로 가지는 결합확률분포이을 쉽게 알 수 있습니다.

큰 문제에 대해서는 위와 같이 바로 transportation plan을 찾기가 어렵습니다. 이를 위해 dual problem을 정의합니다. 모든 최적화 문제는 dual problem이 존재합니다. (문제에 따라 강쌍대성과 약쌍대성을 만족합니다.) 위 문제의 dual 문제는 다음과 같이 쓸 수 있습니다.

$max_{y} \tilde c = b^T y$

s.t. $A^Ty \le d$

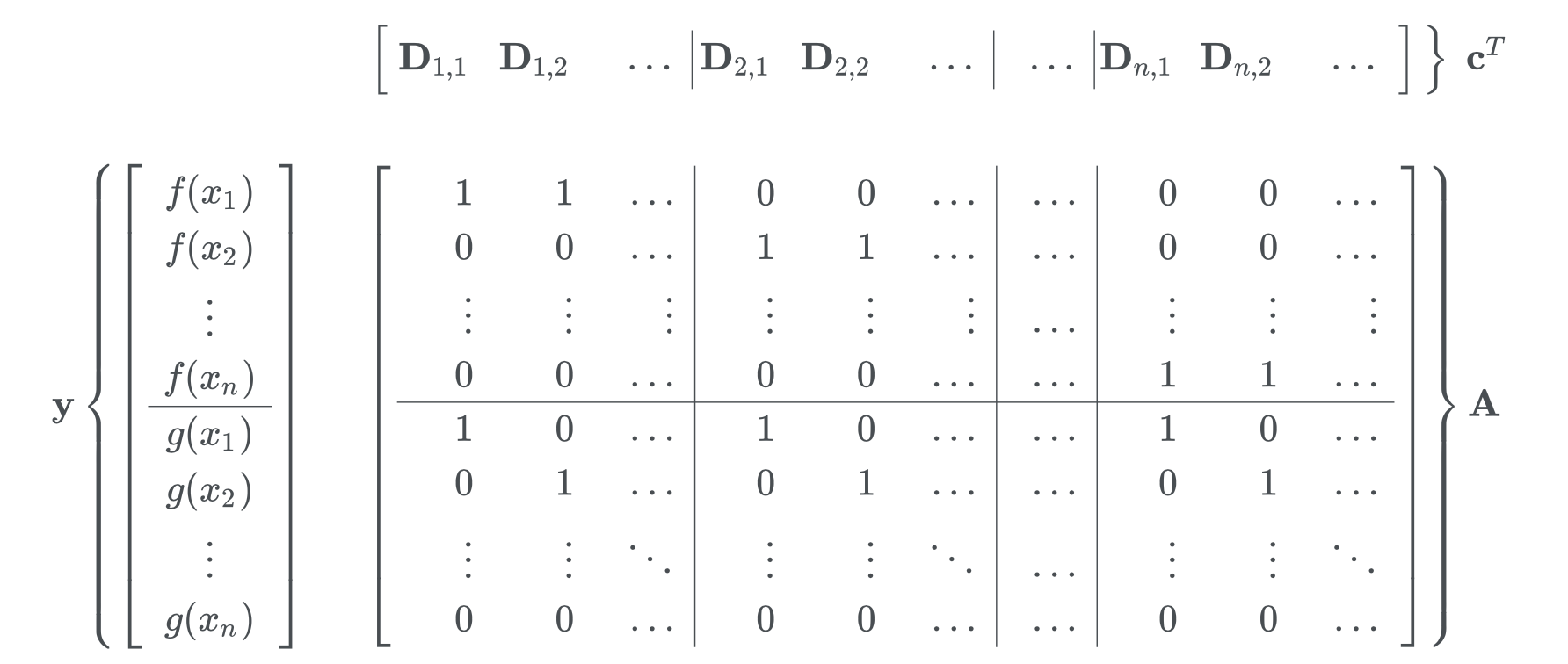
Wasserstein_Dual_Design

원래 도출했던 최적화 문제를 primary form이라 하고, 바로 위에 정의된 문제는 dual form이라고 합니다.

Kantorvich의 formulation은 linear programming의 정준(canonical) 형태로 나타낼 수 있고, 이는 강쌍대성(strong duality)이 성립합니다. 강쌍대성을 가지는 문제는 primary/dual 문제로부터 얻은 solution이 일치한다는 것을 의미하고 우리는 두개의 문제 중에 보다 해를 찾아내기 쉬운 문제를 풀면 됩니다. 이 문제에서는 목적식에 $P_r$과 $P_\theta$가 나타나므로, dual form이 더욱 직관적입니다.

dual form에서 목적함수의 최대값, $\tilde c = b^T y^* $를 다음과 같이 표현할 수 있습니다. $y^* = \left(\begin{array}{c} \boldsymbol f \\ \bf g\end{array}\right)$ $\boldsymbol f$와 $\boldsymbol g$는 각각 $\mathbb R^l$에 속해 있습니다. 목적함수를 다음과 같이 표현할 수 있습니다.

$\tilde c = \sup \boldsymbol f ^T P_\theta + \boldsymbol g P_r$

제약식 $A^Ty$으로부터 다음의 관계를 얻을 수 있습니다.

$f(x_i) + g(x_i) \le D_{i,i}$

$D_{i,i}$는 모든 $i$에 대해서 0입니다. 자기 자신과의 거리는 0이기 때문입니다.

$P_\theta$와 $P_r$이 모두 양의 값을 가지므로 (확률의 공리입니다.) EMD를 극대화하기 위해서는 $\boldsymbol f^T P_\theta + \boldsymbol g^T P_r$이 극대화되는 점이 곧 EMD가 극대화되는 점이고, $f(x_i) \le -g(x_i)$이므로, $f(x_i) = - g(x_i)$인 점에서 극대화 되고, 결국 $\boldsymbol f^T P_\theta + \boldsymbol g^T P_r$은 0인 경우 EMD가 가장 극대화됩니다. (여기서 EMD를 극대화시킨다는 것은 dual 공간에서 작업하기 때문입니다.)

이 조건을 활용하면, 제약식을 다음과 같이 쓸 수 있게 됩니다.

$f(x_i) - f(x_j) \le D_{i, j}$

다시 말하면, 위의 조건을 만족하는 함수족에 대해서 EMD를 극대화하면 된다는 것을 의미합니다. 거기다 EMD 또한 다음과 같이 쓸 수 있습니다.

$\tilde c = f^T P_\theta - f^T p_r = E_{P_\theta}(f) - E_{P_r}(f)$

요약하면, EMD를 구함에 있어서, 모든 가능한 joint distribution의 모임에서 cost를 가장 작게 하는 joint distribution을 골라서, 그 joint distribution에 대해 기대값을 구해야 하는 작업을, Lipschitz 조건을 만족하는 함수족 중 $E_{P_\theta} (f) - E_{P_r}(f)$를 가장 크게 하는 함수를 찾고 그 함수에 대한 기대값을 구하는 문제로 전환한 것입니다.

지금까지 설명해 놓은 Kantorovich-Rubinstein duality에 의한 W-거리는 다음과 같이 정의됩니다.

$W(P_r, P_\theta) = \sup_{\|f\| \le 1} E_{X\sim P_r}(f(X)) - E_{X\sim P_\theta}(f(X))$

이렇게 정의함으로써 우리는 모든 transportation에 대한 $\inf$를 구하지 않아도 됩니다. Lipschitz continuous 함수 중에서 가장 주어진 분포 하에서 기대값을 가장 크게 하는 값이 W-거리가 됩니다. $K$- Lipschitz continuous 함수는

$|f(x) - f(y) | \le K |x - y|$

과 같이 정의된 함수로서 함수가 정의된 모든 점에서 함수의 기울기가 $K$보다 작은 함수를 의미합니다. 참고로 이 함수족은 continuous 할 필요는 없습니다.

다음이 성립합니다.

$\sup_{\|f\| \le K} E_{X\sim P_r}(f(X)) - E_{X\sim P_\theta}(f(X)) = K\cdot W(P_r, P_\theta)$

만약 $K$ - Lipschitz 함수족으로 거리를 정의한다면, 이는 W-거리의 $K$배로 정의가 됩니다.

이제 WGAN에 어떻게 위의 거리가 적용되는지를 살펴보겠습니다.

WGAN의 학습 알고리즘

여전히 Lipschitz 조건을 만족하는 함수의 모임은 너무나 큽니다. 그렇기 때문에 모든 Lipschitz 조건을 만족하는 함수보다는 특정 parameter, $w$로 표현할 수 있는 함수만을 고려합니다. 그리고 이 함수가 $| f_w| \le 1$을 만족한다고 하죠. 만약 parameter의 공간을 $\mathcal W$라고 하면 다음의 관계를 생각할 수 있습니다.

$\sup_{w \in \mathcal W} E_{P_r}(f_w(X)) - E_{P_\theta}(f_w(x)) \le \sup_{\|f\| \le K} E_{X\sim P_r}(f(X)) - E_{X\sim P_\theta}(f(X)) = (a)$

만약 운이 좋게도 $f_w$가 Lipschitz 함수족 중에 (a)를 극대화하는 경우라면 정확하게 W-거리를 찾을 수 있겠지만, 그 자체는 거의 불가능하다고 생각이 됩니다. 하지만 computing cost를 고려한 현실적인 대안으로 여긴다면, 적절한 근사값이 될 수도 있을 것 같습니다.

만약 $f_w$가 W-거리를 적당하게 잘 measure했다면, 이를 바탕으로 Loss의 gradient를 구할 수 있을텐데, 다음과 같이 $\theta$에 대해 편미분을 하면 첫번째 항은 $\theta$와 상관이 없으므로 사라지고, 두번째 항만 남습니다.

$\frac{\partial}{\partial \theta}\sup_{w \in \mathcal W}E_{X\sim P_r}(f(X)) - E_{X\sim P_\theta}(f(X)) = - \frac{\partial}{\partial \theta} E_{P_\theta}(f_w(x)) = -E_{P_\theta}\left(\nabla f_w(x)\right)$

위의 식에 근거해서 모수 $\theta$를 학습하게 되는거죠.

기존의 GAN에서는 discrimator가 있어서, fake와 real의 분포를 보고 생성된 데이터가 real인지 fake인지 판단을 합니다. 하지만, WGAN에서는 그렇게 이분법적으로 판단하는 것이 아니라, 얼마나 실제와 유사한지를 W-거리를 재어 그 거리를 줄여주는 방향으로 generator를 업데이트 합니다.

	GAN	WGAN
Discriminator	JS divergence를 통해 판별기를 학습	$\cdot$
Critique	$\cdot$	Wassersten 거리를 구하기 위한 Lipschtz 함수를 근사
Generator	판별 결과를 1에 가깝도록 학습	데이터 분포와의 W 거리를 줄이는 방향으로 학습

요약하면, 다음과 같은 순서를 따릅니다.

$\theta$가 고정된 상태에서 $W(P_r, P_\theta)$를 구합니다. 거리를 가장 잘 구하기 위해서는 $E_{X\sim P_r}(f_w(X)) - E_{X \sim P_\theta}(f_w(X))$의 supremum을 구해야 하므로, 목적함수를 증가시키는 방향으로 $f_w$의 모수인 $w$를 학습시킵니다. 정확한 거리를 재기 위한 단계입니다.
$f_w$가 어느정도 수렴한 후에는, 다시 말하면, 나름 정확한 W 거리를 찾고 나면, 이 함수를 이용해서 목적함수의 gradient인 $- E_{P_\theta}(\nabla f_w(x))$를 추정합니다. 이때에는 거리를 최소화 해야 하므로, 목적함수를 줄이는 방향으로 $\theta$를 학습합니다.

다음은 논문에서 제시된 알고리즘입니다.

wgan_algorithm

마치며

다음 글에서는 실제 구현체를 통해 WGAN이 어떻게 coding되는지 알아보도록 하겠습니다.

참고문헌

https://www.cph-ai-lab.com/wasserstein-gan-wgan
https://vincentherrmann.github.io/blog/wasserstein/
https://www.alexirpan.com/2017/02/22/wasserstein-gan.html

Back to Posts

GAN과 WGAN 사이 - II

시작하며..

Kantorvich - Rubinstein Duality

WGAN의 학습 알고리즘

마치며

참고문헌

컨볼루션 연산에 대해

Sentiment Analysis - MLP