WGAN
WGAN은 기존의 $f-GAN$의 확장으로 볼 수 있는 GAN의 많은 variant 중의 하나입니다. 2014년 GAN이 세상에 선을 보인 후로, GAN이 변형된 수많은 모형들이 나왔습니다. 그 중 Google의 DC-GAN이 안정적인 학습을 위한 guide line을 제시하였다면, WGAN은 학습이 잘 안되는 이유를 KL divergence의 한계로 언급하며, loss function을 재정의하여 안정성을 제고합니다. 여기에서는 Wasserstein distance에 대해서 자세히 알아보도록 하겠습니다.
GAN의 loss
Ian Goodfellow의 14년 논문인 GAN에서는 discriminator와 generator의 상호작용을 통해 generator 신경망을 학습하는 알고리즘이 소개되어 있습니다. Deep learning의 선구자 중 하나인 Yann LeCun가 과거 10년 간 machine learning 분야에서 나온 idea 중의 최고의 아이디어 중 하나라고 칭송했던 GAN은 다음의 loss function을 최소화 하도록 학습을 합니다.
위의 식에서 $D$는 판별기(discriminator)를, $G$는 생성기(generator)를 의미합니다. $X$는 데이터 공간에서의 확률변수를, $Z$는 분석가가 임의로 설정한 공간에서의 확률변수입니다. 이쯤에서 그 흔한 GAN의 개념도 한번 보여드려야겠습니다.
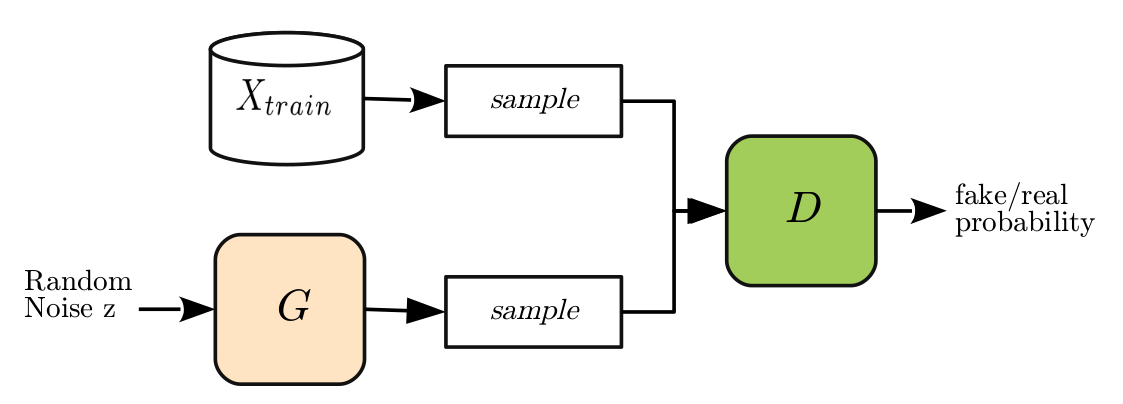
Random noise가 생성기를 통과해서 나온 생성된 가짜 표본을 진짜 표본으로부터 분리하는 판별기가 있습니다. 이런 상황에서 판별기는 판별기대로, 진짜와 가짜를 잘 구분하기 위해서, 생성기는 생성기대로 판별기를 잘 속일 수 있는 진짜와 같은 데이터를 만들어내려고 노력하는 모습입니다. 결국
이 되는 것이 목표입니다.
위의 손실함수는 두개의 최적화 문제가 중첩되어 있는 구조입니다. 위의 손실함수를, 판별기($D$)에 대해서는 최대화하고, 생성기($G$)에 대해서는 최소화해야 합니다. 두개의 상반되는 목적을 지녔으므로, “adversarial”이라는 단어가 붙은 것이겠죠. 사실 논문에서는 위의 손실함수를 “game theoretic”이라는 어려운 말을 써가면서 설명하지만, 실제 학습은 두개의 최적화 과제를 번갈아 가면서 수행을 합니다.
예를 들면, 먼저 $G$를 고정시킵니다. 그런 다음, 임의의 noise (noise의 차원은 분석가가 정합니다.)인 $z$를 생성기 $G$에 넣어서 얻은 생성 데이터의 판별값은 0에 가깝게, 실제 데이터를 판별기가 판별한 값은 1에 가깝게 판별기($D$)를 학습합니다. 보통은 손실함수의 최소값을 구하는데, GAN에서는 최대값을 구합니다. 의아하다고 생각해서 자세히 봤더니, 최대화하는 대상이 일반적인 손실함수와는 반대방향으로 표현되어 있습니다.
그런 후에 판별기를 고정시킨 후 생성기($G$)를 학습시키되, 손실함수를 작게 하도록 학습합니다. 만약 생성기가 지난 스텝보다 조금더 생성을 잘 한다면, $D(G(Z))$는 1에 좀더 가까워질 것이고, 그러면 손실함수의 두번째 항의 값은 조금 더 작아지겠죠. 첫번째 항에는 생성기($G$)가 없으므로, 생성기를 최적화시키는 단계에서는 상수의 역할을 합니다. 위의 수식에서 기대값이 눈에 살짝 거슬리기는 하는데, 각각 데이터의 분포와 잠재변수의 분포에 대해 기대값을 취하라는 의미로, empirical distribution에 대한 기대값을 의미하고 이는 그냥 여러 표본으로부터 나오는 loss값을 평균하라는 의미입니다.
WGAN을 설명하기 전에 이렇게 장황하게 GAN의 손실함수를 다시 이야기하는 것은 GAN의 손실함수의 목적이 무엇인지 언급하기 위한 것입니다. $n$개의 데이터가 주어져 있는 상황에서, 로그 우도함수는 다음과 같이 정의됩니다. 여기서 $P$는 확률밀도함수(pdf) 혹은 확률질량함수(pmf)를 의미합니다.
위의 로그우도함수를 극대화하는 것은 다음과 같이 바꿔 쓸 수 있습니다.
여기서 알아야 할 것은 우리의 관심사는 $\theta$라는 것입니다. 데이터 포인트는 주어져 있는 것이므로,
위의 식에서 하고자 하는 말은, 로그우도함수를 최대화 것은 곧 KL Divergence를 최소화 하는 것이라는 겁니다.
또한 14년 논문에서는 위의 손실함수가 생성기가 완전하게 판별기를 속이는 상황 하에서는 Jensen Shannon divergence와 일치한다는 것을 증명합니다.
크게 어렵지 않은 도출 과정이지만, 위의 derivation은 좋은 insight를 주는데요. 바로 GAN이 학습하기 어려운 이유를 말해주기 때문입니다. 로그우도함수 그 자체를 추정하는 것이 KL divergence가 fail하면 어려워질 수 있다는 것을 의미하기도 합니다.
GAN이 가장 해결해야 할 문제로, 잘 학습이 안된다는 문제입니다. DCGAN이 나옴으로써 이미지에서는 어느정도 해결된 문제이기는 하지만 여전히 mode collpase라는 문제를 가지고 있습니다. mode collapse를 쉽게 설명하자면, 비슷한 이미지만 계속 만드는 현상이라고 생각할 수 있습니다. MNIST를 예로 들면 생성기가 만약 6이라는 숫자만 잘 만들어 낸다고 하면, 판별기의 입장에서는 6만 가짜라고 생각을 하고 나머지 숫자들은 모두 진짜라고 생각해버릴 수 있다는 겁니다. 그렇게 된느 순간 판별기는 진짜/가짜를 판별하는 것이 아니라 6인가 6이 아닌가를 판별하는 판별기로 변해 버리는 것입니다. 그러한 판별기에 맞추기 위해 생성기는 다시 6이 아닌 다른 숫자를 만들어내기 시작하겠죠. 어떻게든 판별기를 속여야 할 테니까요. 그렇게 해서 다시 예를 들어 8이라는 숫자를 만들어내기 시작하고 판별기는 생성기한테 속지 않기 위해 다시 8인지 아닌지를 판별하는 판별기로 바뀝니다. 이런 현상은 0에서 9까지 모든 숫자에 대해 (모든 숫자는 아닐 수 있습니다.) 반복되게 되는데요. 이를 mode collapse 문제라고 합니다. 아래의 그림은 Improved Training of Generative Adversarial Networks using Representative Features라는 논문에 실린 그림인데, GAN의 mode collapse 문제를 보여줍니다.
이러한 이유 중의 하나로 손실함수의 distance measure로 보는 시각이 있는데요. 그래서 나온 것이 WGAN입니다. WGAN에서는 GAN이라는 distance measure가 적합하지 않을 수 있다라고 이야기 합니다. 그 이유는 KL divergence도 마찬가지이지만, JS divergence는 비교하는 두개의 분포가 같은 support를 가져야 하기 때문입니다. KL divergence의 정의를 보면 금방 확인할 수 있습니다.
$p_A(x) = 0$인 점이면 어차피 확률 밀도가 없으므로 상관 없겠습니다만, $p_A(x) > 0 $인 어떤 주어진 점 $x$에서 확률밀도 함수의 비율이 정의되려면, $p_A(x)$가 0이 아닌 곳에서는 $p_B(x)$가 0이 되어서는 안되기 때문입니다.
manifold hypothesis 관점에서 보면, 데이터 공간에 비해 데이터를 잘 표한하는 의미있는 manifold는 극히 작은 공간에 몰려있고, 데이터의 분포와 생성된 결과의 분포의 support가 겹치지 않을 확률이 아주 높다고 볼 수 있겠습니다. 만약 그런 경우, 손실함수가 실제 데이터 분포와 생성된 데이터 분포 간의 거리를 제대로 표현하지 못하게 되고, 결국 gradient가 모수를 제대로 업데이트 하지 못하게 됩니다. 그래서 수렴이 어려울 수 있다고 WGAN의 저자들은 주장합니다.
새로운 거리 정의
결국 JS divergence보다는 더 정의가 되기 쉽고 JS divergence보다 수렴도 잘 되는 거리를 찾고 싶습니다. 아시다시피 확률변수, 확률분포의 수렴에 관해서는 여러가지 척도가 있습니다. 확률공간에서 확률변수와 확률분포간의 수렴 관계가 정리되어 있는 그림을 google에서 찾았습니다.
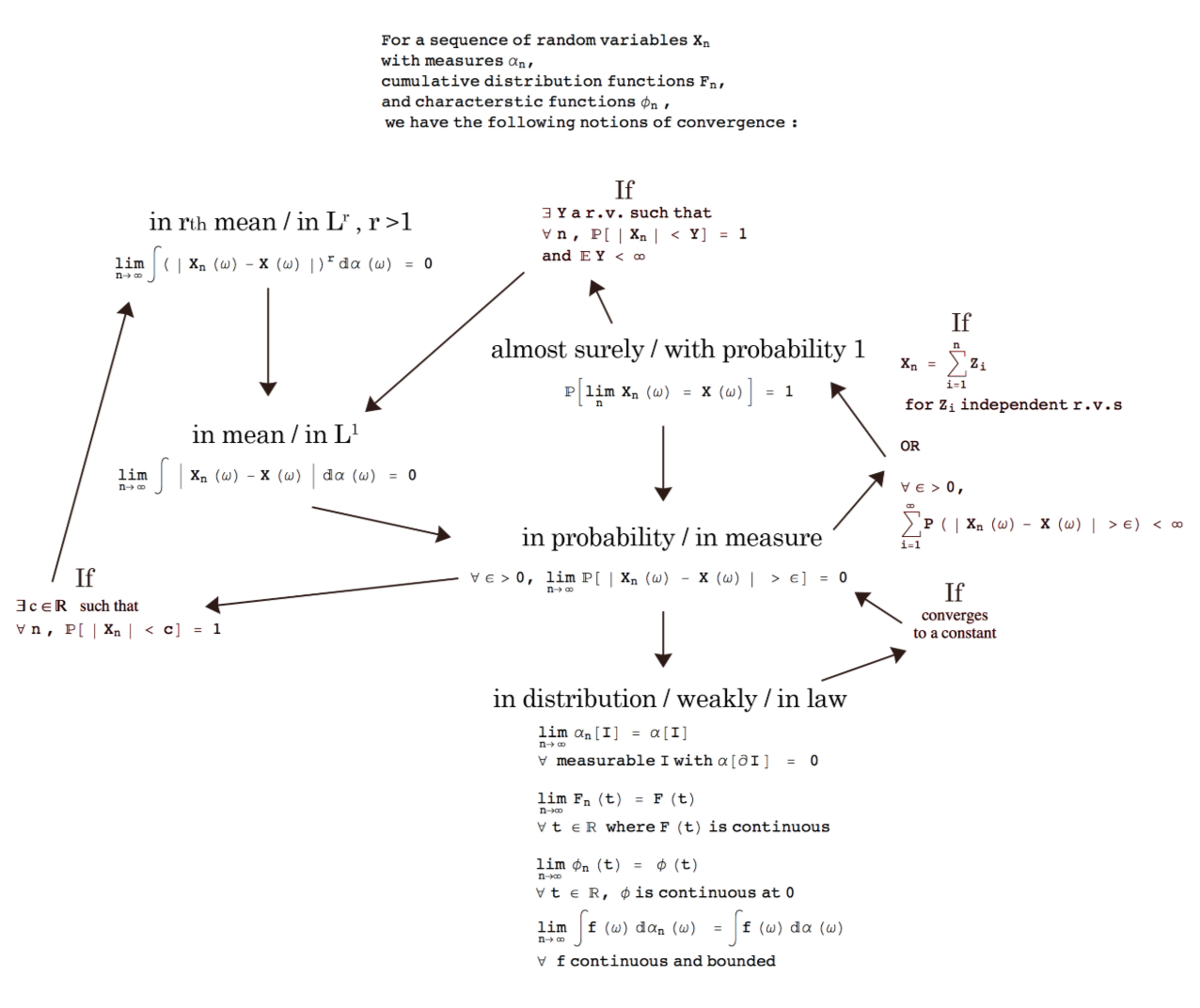
확률변수가 존재하면, 그 확률변수를 표현하는 확률분포를 만들 수 있습니다. 확률변수 자체는 어떠한 데이터 공간에도 정의할 수 있지만, 확률분포 함수는 실수에서 정의됩니다. 따라서 우리가 확률변수와 분포에 대해서 이야기 할 때, 따로 구분하지 않아 거의 비슷한 개념으로 여기기 쉽지만, 확률변수와 확률분포가 완전히 같은 개념을 말하는 것은 아닙니다. 따라서 확률 변수의 수렴과 확률분포의 수렴은 꼭 일치할 필요가 없습니다. 예를 들면, 강아지의 몸무게도 정규분포를 따를 수 있고, 사람의 몸무게도 정규분포를 가질 수 있다는 거죠. 두 개의 확률변수는 전혀 다른 확률변수이지만 동일한 정규분포라는 함수로 표현이 됩니다. 이는 곧 확률 분포함수가 수렴을 한다고 해도 확률변수는 수렴을 할 필요가 없다는 것입니다. 간단한 toy example로 다음을 생각해 보겠습니다. 아주 단순한 표본 공간에 $a$와 $b$라는 두점이 존재하고 각각의 확률은 0.5라고 생각해 보겠습니다. 이러한 표본 공간에서에서 확률변수 두개를 다음과 같이 정의합니다.
$n$에 상관없이, $X_n$과 $Y$는 다음고 같은 동일한 누적확률분포를 가집니다.
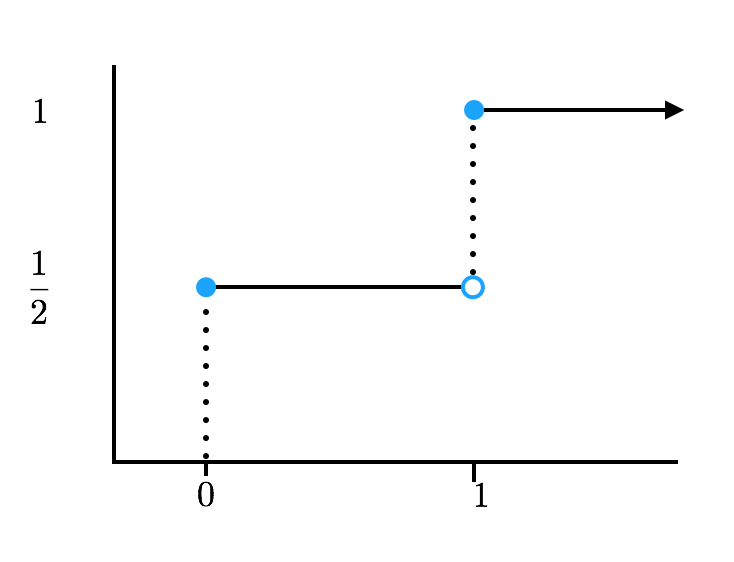
하지만 두 확률 변수는 언제나 거리가 1입니다.
두 점에서 모두 같은 현상이 발생하죠. 다음과 같이 쓸 수 있습니다.
확률변수의 확률 수렴은 다음과 같이 정의됩니다. 확률변수의 sequence, $X_1, X_2, \ldots$와 $X$에 대해
이면 확률변수열 $X_n, n = 1, \ldots $,가 $X$로 수렴한다고 이야기 합니다. $\epsilon$은 0에 무한히 작은 임의의 숫자입니다. 아무리 작은 숫자를 가져와도 그 숫자보다 차이가 클 확률은 0이라는 것입니다.
하지만 위의 식에서 보면, 심지어 $\epsilon$을 0.99와 같이 큰 수로 잡아도 확률은 언제나 1입니다. 따라서, 확률변수 $X_n$은 $Y$로 수렴하지 않습니다. 동일한 확률 분포를 가지는 데도 말입니다.
확률변수와 확률분포의 관계는 확률론에서는 중요하게 다루는 수렴관계이지만, ML에서는 그렇게 크게 관심을 가지지 않습니다. ML에서는 확률 변수의 수렴 보다는 확률 분포 함수의 수렴에 좀더 중점을 둡니다. 어차피 확률론의 중요한 테마 중의 하나인 확률분포는 수렴하지만 확률변수는 수렴하지 않는 상황을 거의 생각조차 하지 않습니다. 엄밀한 수렴성에는 아직 관심을 가질만큼 이론적으로 다듬어지지 않았다고도 생각할 수 있겠습니다. 어쨌든, 이런 저런 이유로 ML에서는 확률변수에 대한 수렴은 그렇게 중요하지 않습니다.
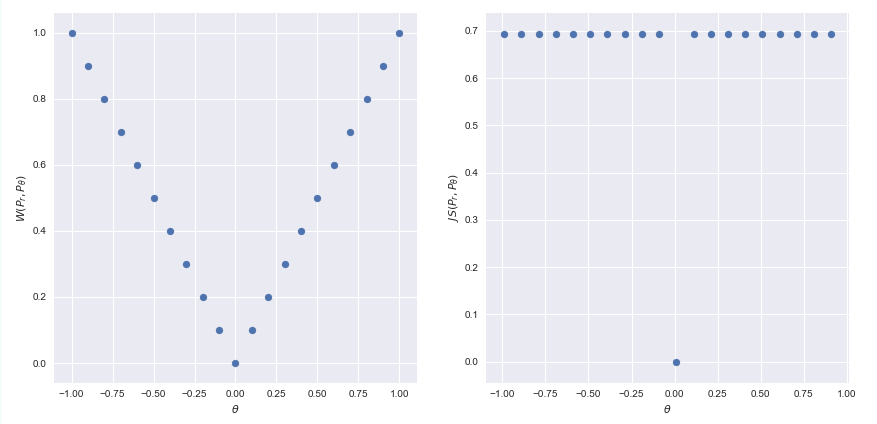
우리의 목표는 어떤 모수를 조정해서, 실제 데이터의 분포와 비슷한 분포를 찾는 것입니다. 모수를 조정하는 방법은 너무나도 익숙(?)한 backpropagation 알고리즘이겠지요. 제대로 모수를 조정해서 데이터의 분포와 비슷한 분포를 만들려고 하면, 모수가 정의하는 분포와 실제 데이터의 분포가 얼마나 비슷한지를 측정해야 할 것입니다. GAN에서는 그 측도로 JS divergence를 쓰게 되었던거죠. 하지만 이 JS divergence가 분포간의 거리를 제대로 설명해주는 measure가 아닐 수도 있다는 것이 WGAN의 주장이구요. WGAN 논문에서는 JS divergence가 실패하는 예로, 2차원 공간에서 정의된 다음과 같은 2개의 분포를 생각합니다.
위의 경우에 3가지 distance를 예로 들었습니다. Total Variation(TV), KL Divergence, JS Divergence입니다. 먼저 TV는
로 정의되는데, 이것을 말로 풀어쓰면, 2차원 평면의 모든 점들의 집합 중에서 분포함수의 차이를 가장 크게 하는 집합 $A$가 주어졌을 때 그 차이를 의미합니다.
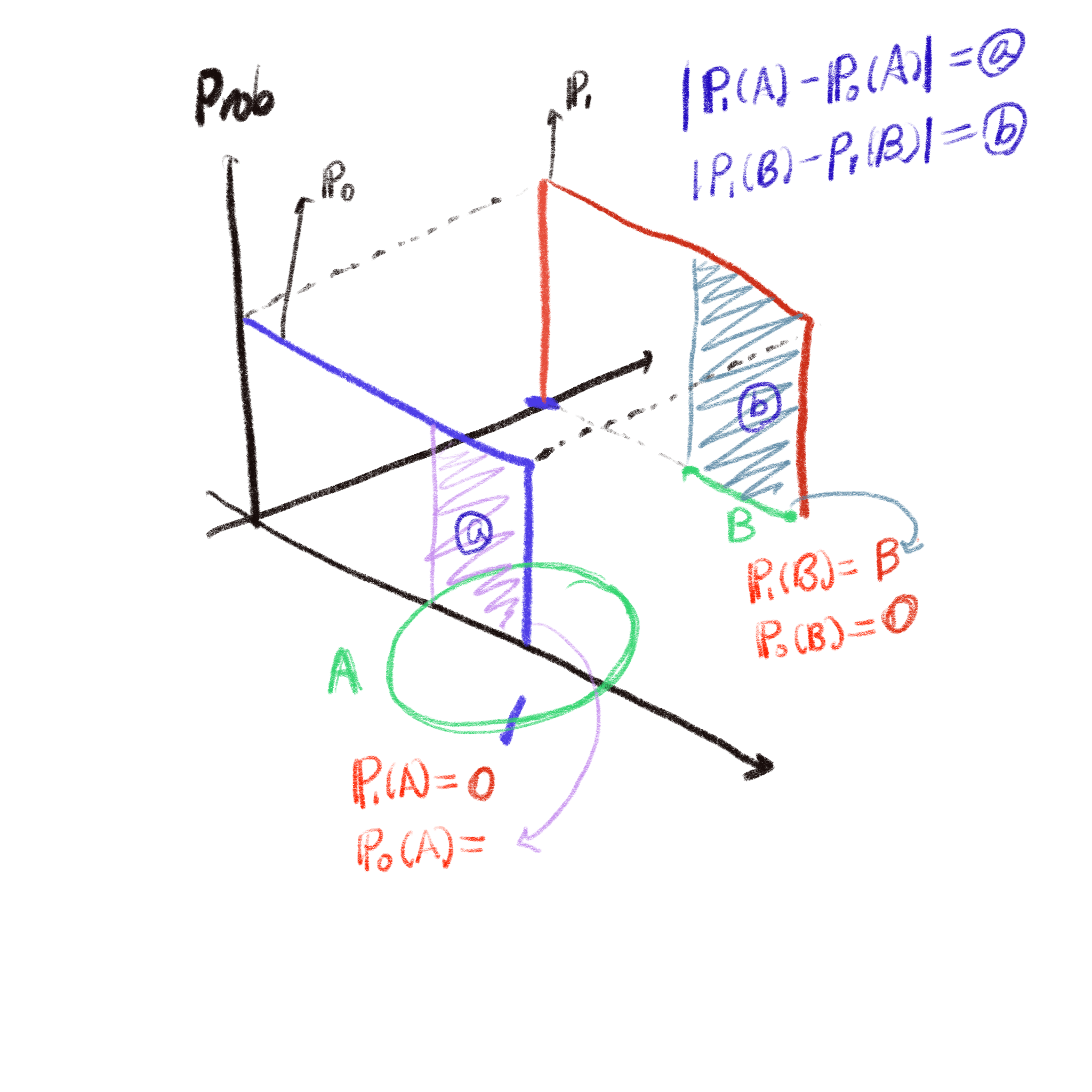위의 그림과 같이 곰곰히 생각해 보면, $\theta = 0$이 아닌 이상 TV는 언제나 1입니다.
KL Divergence는 아예 정의가 되지 않습니다. $\mathbb P_1(A) = 0$인 곳에서는 언제나 $\mathbb P_0(A) = 0$이기 때문입니다.
마찬가지로 JS Divergence는 KL보다 나은 게 언제나 $\theta$가 0이 아닌 어느 곳에서도 거리는 $\log 2$입니다. KL Divergence보다 좀 낫기는 하지만, 두 분포의 거리는 $\theta$에 대한 적절한 정보를 주지 못합니다. 신경망의 모수를 얼만큼 움직이면 (여기서는 $\theta$를 얼만큼 움직이면), 두 분포의 거리가 얼마가 변할 거라는 정보를 담고 있어야 하는 gradient는 $\theta$가 0이 되는 순간 모수를 옮길 필요 없이 분포의 거리가 0이라는 사실만을 말해줄 뿐, $\theta$가 0이 아니라면 언제나 $\log 2$라는 값을 내뱉습니다. $\theta$를 얼마나 바꿔야 할지에 대한 정보가 없습니다.
마지막으로 보여주는 예가 Wasserstein distance인데요. 자세한 원리에 대해서는 뒷부분에서 설명드리겠지만, 위 두 분포 간의 W-거리는 다음과 같이 정의됩니다.
비로소 W-거리에 바탕하면, 두 분포를 일치시키기 위해서는 $\theta$를 0 방향으로 움직여야 함을 알 수 있게 됩니다.
다음은 논문의 해당부분입니다.
W-distance의 유용성을 알았습니다. 그렇다면 본격적으로 W-distance의 정의에 대해서 알아보도록 하겠습니다.
Wasserstein distance
두개의 분포 $P_r$와 $P_\theta$ 사이의 거리를 재는 방법은 여러가지가 있습니다. 분포 간의 거리를 재는 Wasserstein distance는 다음과 같이 정의됩니다.
NOTE: $\inf$는 largest lower bound로 정의됩니다. 최소값이 해당 셋에 존재하지 않는다 하더라도 정의되는 최소값에 해당하는 가장 근접한 값이라고 보면 되겠습니다. 가장 단순한 예로 $f(x) = \frac 1 {1 + exp (-x)}$의 최소값은 무엇일가요? $x$가 음의 무한대로 가도 위의 함수는 0에 도달할 수 없습니다. 영원히 가까워져 갈 뿐이죠. 이런 경우 $f(x)$의 최소값, $\min_{x\in [0,\infty)} f(x)$은 0이라는 말을 할 수 없습니다. 왜냐하면, 0이라는 숫자는 $f(x)$의 치역(range)인 $(0, \infty)$이라는 set의 바깥에 있기 때문입니다. 반면, $\inf_{x\in [0,\infty)} f(x) = 0$이라고 할 수는 있습니다. 이렇게 수학적으로 보다 완전성을 기하기 위한 표현이라고 보시면 됩니다. 어차피 discrete한 세상에서 사는 data scientist들은 그냥 단순하게 $\min$로 생각해도 될 것 같습니다.
Wasserstein distance는 두개의 주변 확률 분포를 일치시키기 위해 하나의 분포를 다른 분포로 변화시키기 위해 mass를 옮기는 과정(transportation plan)을 상상합니다. 머신러닝 분야에서는 이 거리를 Earth Moving distance라고 하는데 mass를 움직임을 은유적으로 표현한 것이 아닌가 싶습니다. 결론부터 말하자면, Transportation plan은 결합확률분포의 다른 표현입니다. 그 이유는 다음과 같습니다.
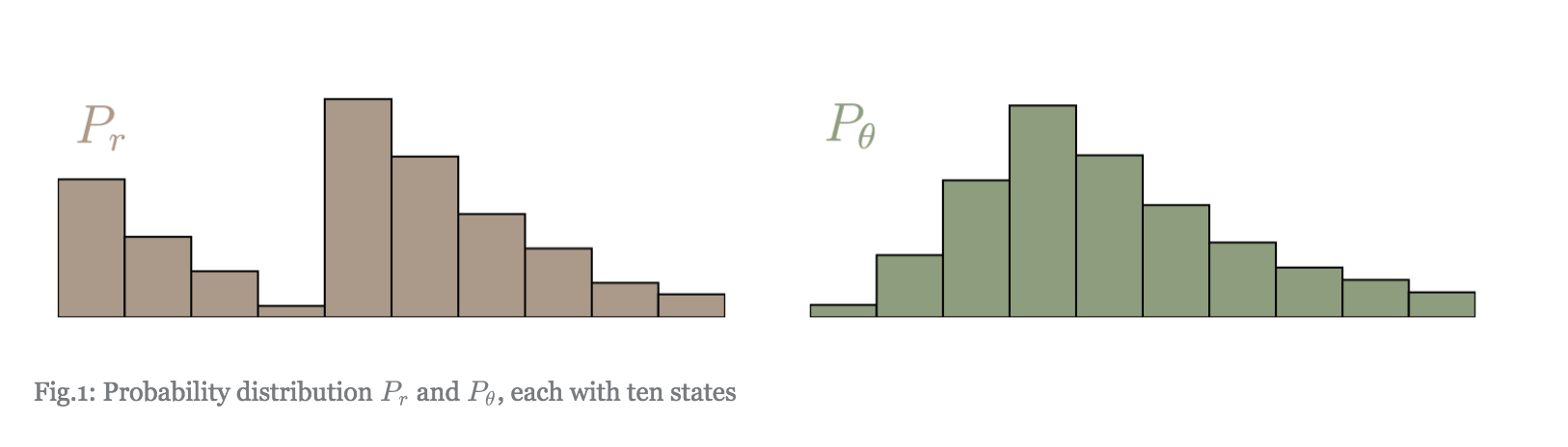
먼저 각각의 분포가 $l$개의 bin으로 구분되어 있다고 생각합니다. $x$를 $P_r$의 support에 있는 bin으로, $y$를 $P_\theta$의 support에 있는 $l$개 bin 중에 하나라고 합니다. $\gamma(x, y)$는 $P_\theta$의 bin $x$로부터 $P_r$의 bin $y$로 움직이는 mass의 크기를 나타냅니다. 예를 들면, $\gamma(1, 3)= .2$는 $P_\theta(1)$의 mass 중 .2를 $P_r(3)$으로 옮기라는 의미입니다. Transportation plan은 다음의 조건을 만족해야 합니다.
위의 조건을 만족하는 모든 원소가 비음(non-negative)인 함수 $\gamma(x, y)$는 결합확률분포의 정의와 정확하게 일치합니다.
문제는 과연 어떻게 어떤 순서로 mass를 움직여야 하는가입니다. mass를 움직이는 방법에는 거의 무한대에 달하는 방법이 있습니다. 통계학에서는 “주변확률 분포가 결합확률분포를 결정할 수 없다”라고 하는데, 정확히 transportation plan이 무한히 있다는 말과 일치합니다. Wasserstein distance는 수많은 transportation plan 중에서 cost를 가장 작게 하는 방법을 바탕으로 두 분포의 거리로 정의합니다. Cost는 mass를 이동해야 하는 거리와 이동해야 하는 mass의 양을 곱한 것입니다.
움직여야 하는 거리는 $|x -y |^p$입니다. 여기서 $|\cdot|^p$는 $p$차 norm을 의미합니다. mass는 위에서 예를 들어 보여드린 것처럼, $\gamma(x,y)$로 표현됩니다. Cost는 다음과 같이 표현할 수 있습니다.
오른편 식을 보면, 변수들이 가질 수 있는 모든 값들의 조합에 대해 확률분포함수와 $|x - y |^p$의 곱을 더해 놓은 것으로 이는 바로 기대값의 정의와 일치합니다. 그래서 Cost는 다음과 같이 기대값으로 쓸 수 있습니다.
다시 말하면, Wasswerstein 거리는 주변분포가 주어져 있을 때, 이 두개의 분포를 주변분포로 하는 결합분포 중에서 $E(|x-y|^p)$를 가장 작게 하는 분포를 골랐을 때, $| x - y|^p$의 기대값입니다.
이제 W-거리가 무엇인지에 대해서 알게 되었습니다. 하지만, 모든 가능한 결합확률 분포 중에 cost를 가장 작게 하는 결합확률분포를 찾아내고, 그 결합확률분포에 대한 기대값을 찾아낸다?! 이건 정말 어렵고 어려운 일 아닐까요? 정의 그대로 W-거리를 계산하다가는 분포 간의 거리를 계산하다, 정작 모수를 update하는 backpropagation은 본격적으로 시작도 해보지 못하고 끝나버리게 될 것 같습니다. 그래서, 이 W-거리를 좀더 쉽게 구할 수 있는 현실적인 대안을 제시하는데요. 다음에는 W-거리를 어떻게 근사하는지, 그리고 그게 어떻게 WGAN에 적용되는지를 알아보도록 하겠습니다.
마치며
너무 dense한 내용이라 이번 글은 여기에서 마치도록 하겠습니다. 너무 짧은가요? 저는 아직도 적당한 블로그의 길이를 모르겠습니다…ㅠㅠ
참고문헌
- https://www.cph-ai-lab.com/wasserstein-gan-wgan
- https://vincentherrmann.github.io/blog/wasserstein/
- https://www.alexirpan.com/2017/02/22/wasserstein-gan.html